Геометрия Римана

Геометрия Римана (называемая также эллиптическая геометрия) — одна из неевклидовых геометрий постоянной кривизны (другие — это геометрия Лобачевского и сферическая геометрия). Если геометрия Евклида реализуется в пространстве с нулевой гауссовой кривизной, Лобачевского — с отрицательной, то геометрия Римана реализуется в пространстве с постоянной положительной кривизной (в двумерном случае — на проективной плоскости и локально на сфере).

В геометрии Римана прямая определяется двумя точками, плоскость — тремя, две плоскости пересекаются по прямой и т. д., но в геометрии Римана нет параллельных прямых. В геометрии Римана, как и в сферической геометрии, справедливо утверждение: сумма углов треугольника больше двух прямых, имеет место формула ${\displaystyle \Sigma =\pi +{S}/{R^{2}},}$ где ${\displaystyle \Sigma }$ — сумма углов треугольника, ${\displaystyle R}$ — радиус сферы, на которой реализована геометрия.

Отождествление противоположных точек сферы в геометрии Римана

Двумерная геометрия Римана похожа на сферическую геометрию, но отличается тем, что любые две «прямые» имеют не две, как в сферической, а только одну точку пересечения. При отождествлении противоположных точек сферы получается проективная плоскость, геометрия которой удовлетворяет аксиомам геометрии Римана.

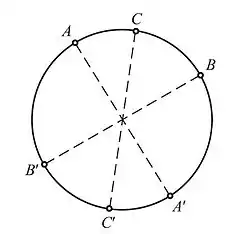
Именно, рассмотрим сферу ${\displaystyle S}$ с центром в точке ${\displaystyle O}$ в трёхмерном пространстве ${\displaystyle E}$. Каждая точка ${\displaystyle A\in S}$ вместе с центром сферы ${\displaystyle O}$ определяет некоторую прямую ${\displaystyle l\subset E}$, то есть некоторую точку ${\displaystyle A_{*}}$ проективной плоскости ${\displaystyle \Pi }$. Сопоставление ${\displaystyle A\to A_{*}}$ определяет отображение ${\displaystyle S\to \Pi }$, большие круги на ${\displaystyle S}$ (прямые в сферической геометрии) переходят в прямые на проективной плоскости ${\displaystyle \Pi }$, при этом в одну точку ${\displaystyle A_{*}\in \Pi }$ переходят ровно две точки сферы: вместе с точкой ${\displaystyle A\in S}$ и диаметрально противоположная ей точка ${\displaystyle A'\in S}$ (см. рисунок). Евклидовы движения пространства ${\displaystyle E}$, переводящие сферу ${\displaystyle S}$ в себя, задают некоторые определенные преобразования проективной плоскости ${\displaystyle \Pi }$, которые являются движениями геометрии Римана. В геометрии Римана любые прямые пересекаются, поскольку это верно для проективной плоскости, и таким образом, в ней нет параллельных прямых.

Одно из отличий геометрии Римана от евклидовой геометрии и геометрии Лобачевского состоит в том, что в ней нет естественного понятия «точка C лежит между точками A и B» (в сферической геометрии это понятие также отсутствует). Действительно, на прямую проективной плоскости ${\displaystyle \Pi }$ отображается большой круг на сфере ${\displaystyle S}$, причём две диаметрально противоположные точки сферы ${\displaystyle A}$ и ${\displaystyle A'}$ переходят в одну точку ${\displaystyle A_{*}\in \Pi }$. Аналогично, точки ${\displaystyle B,B'}$ переходят в одну точку ${\displaystyle B_{*}\in \Pi }$ и точки ${\displaystyle C,C'}$ переходят в одну точку ${\displaystyle C_{*}\in \Pi }$. Таким образом, с равным основанием можно считать, что точка ${\displaystyle C_{*}}$ лежит между ${\displaystyle A_{*}}$ и ${\displaystyle B_{*}}$ и что она не лежит между ними (см. рисунок).