T-раскраска

T-раскраска графа $G=(V,E)$ , заданная множеством T неотрицательных целых, содержащим 0, — это функция $c:V(G)\rightarrow \mathbb {N}$ , которая отображает каждую вершину графа G в положительное целое (цвет) так, что $(u,w)\in E(G)\Rightarrow \left|c(u)-c(w)\right|\notin T$ [1]. Простыми словами, абсолютное значение разности между двумя цветами смежных вершин должно не принадлежать фиксированному множеству T. Концепцию предложил Уильям К. Хейл[2]. Если T = {0}, это сводится к обычной раскраске вершин.

Две T-раскраски графа для T = {0, 1, 4}

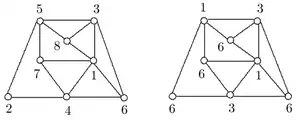
Дополняющая раскраска T-раскраски c, которая обозначается как ${\overline {c}}$ , определяется для каждой вершины v графа G как
${\overline {c}}(v)=s+1-c(v)$
, где s — наибольший номер цвета, назначенные вершине графа G функцией c[1].

T-хроматическое число

T-хроматическое число $\chi _{T}(G)$ — это число цветов, которые могут быть использованы для T-раскраски графа G. T-хроматическое число равно хроматическому числу, $\chi _{T}(G)=\chi (G)$ [3].

Доказательство

Любая T-раскраска графа G является также раскраской вершин графа G, такая, что $\chi _{T}(G)\geqslant \chi (G)$ . Предположим, что $\chi (G)=k$ и $r=max(T)$ .

Если дана функция k-раскраски вершин $c:V(G)\rightarrow \mathbb {N}$ с в цвета 1, 2,..,k.

Мы определим $d:V(G)\rightarrow \mathbb {N}$ как

d(v)=(r+1)c(v)

.

Для любых двух смежных вершин u и w графа G

\left|d(u)-d(w)\right|=\left|(r+1)c(u)-(r+1)c(w)\right|

=(r+1)\left|c(u)-c(w)\right|\geqslant r+1

,

так что $\left|d(u)-d(w)\right|\notin T$ .

Таким образом, d является T-раскраской графа G. Поскольку d использует k цветов, $\chi _{T}(G)\leqslant k=\chi (G)$ .

Следовательно, $\chi _{T}(G)=\chi (G)$ ■

T-размах

Для T-раскраски c графа G, c-размах $sp_{T}(c)=\max\{|c(u)-c(w)|\}$ по всем $uw\in$ V(G).

T-размах $sp_{T}(G)$ графа G — это $\min\{sp_{T}(c)\}$ всех раскрасок c графа G[4]

Некоторые границы T-размаха даны ниже:

Для любой k-раскраски графа G с кликой размера $\omega$ и любого конечного множества T неотрицательных целых чисел, содержащего 0, $sp_{T}(K_{\omega })\leqslant sp_{T}(G)\leqslant sp_{T}(K_{k})$ .

Для любого графа G и любого конечного множества T неотрицательных целых чисел, содержащего 0, наибольшим элементом которого является r, $sp_{T}(G)\leqslant (\chi (G)-1)(r+1)$ , $\chi _{T}(G)=\chi (G)$ [5].
Для любого графа G и любого конечного множеств T неотрицательных целых чисел, содержащего 0, мощность которого равна t, $sp_{T}(G)\leqslant (\chi (G)-1)t$ . $\chi _{T}(G)=\chi (G)$ [5].

Примечания

Chartrand, Zhang, 2009, с. 397–402.
Hale, 1980, с. 1497–1514.
Cozzens, Roberts, 1982, с. 191–208.
Chartrand, Zhang, 2009, с. 399.
Cozzens, Roberts, 1982, с. 191–208.

Литература

Gary Chartrand, Ping Zhang. 14. Colorings, Distance, and Domination // Chromatic Graph Theory. — CRC Press, 2009.
Hale W. K. Frequency assignment: Theory and applications // Proc. IEEE. — 1980. — Т. 68.
Cozzens M. B., Roberts F. S. T -colorings of graphs and the Channel Assignment Problem // Congr. Numer.. — 1982. — Вып. 35.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_e4b5e7bd94cce5fd-1] Chartrand, Zhang, 2009, с. 397–402.

[_5e60f83208820eb8-2] Hale, 1980, с. 1497–1514.

[_ed8ec2a51fce49da-3] Cozzens, Roberts, 1982, с. 191–208.

[_f0c719d79ffee00e-4] Chartrand, Zhang, 2009, с. 399.

[_20cc76499d3a9124-5] Cozzens, Roberts, 1982, с. 191–208.