10-клетка Балабана
10-Клетка Балабана или балабанова (3,10)-клетка — это 3-регулярный граф с 70 вершинами и 105 рёбрами, названный именем химика румынского происхождения А.Т. Балабана [1]. Опубликован в 1972[2]. Это была первая обнаруженная (3,10)-клетка, но не единственная[3].
| 10-клетка Балабана | |
|---|---|
 | |
| Назван в честь | А.Т. Балабана |
| Вершин | 70 |
| Рёбер | 105 |
| Радиус | 6 |
| Диаметр | 6 |
| Обхват | 10 |
| Автоморфизмы | 80 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Свойства |
Кубический Клетка Гамильтонов |
(3-10)-клетки
Полный список (3-10)-клеток дали и доказали минимальность О'Кииф и Вонг[4]. Существует 3 различные (3-10)-клетки, две другие — граф Харриса и граф Харриса – Вонга[5]. Однако граф Харриса – Вонга и граф Харриса — являются коспектральными.
Свойства
10-Клетка Балабана имеет хроматическое число 2, хроматический индекс 3, диаметр 6, обхват 10 и граф является гамильтоновым. Граф является также вершинно 3-связным и рёберно 3-связным.
Характеристический многочлен 10-клетки Балабана равен
Галерея
 Хроматическое число 10-клетки Балабана равно 2.
Хроматическое число 10-клетки Балабана равно 2.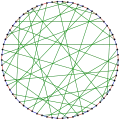 Хроматический индекс 10-клетки Балабана равен 3.
Хроматический индекс 10-клетки Балабана равен 3. Альтернативное представление 10-клетки Балабана.
Альтернативное представление 10-клетки Балабана.
См. также
Примечания
- Weisstein, Eric W. Balaban 10-Cage (англ.) на сайте Wolfram MathWorld.
- Balaban, 1972, с. 1-5.
- Pisanski, Boben, Marušič, Orbanić, 2001.
- O'Keefe, Wong, 1980, с. 91–105.
- Bondy, Murty, 1976, с. 237.
Литература
- A. T. Balaban. A trivalent graph of girth ten // J. Combin. Theory. — 1972. — Вып. 12.
- M. O'Keefe, P.K. Wong. A smallest graph of girth 10 and valency 3 // J. Combin. Theory. — 1980. — Вып. 29.
- T. Pisanski, M. Boben, D. Marušič, A. Orbanić. The Generalized Balaban Configurations. — 2001. — Т. 39. — ISSN 1318-4865.
- J. A. Bondy, U. S. R. Murty. Graph Theory with Applications. — New York: North Holland, 1976. — ISBN 0-444-19451-7.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.