Эффект Гуржи

Эффект Гуржи был теоретически предсказан[1][2] Радием Николаевичем Гуржи в 1963 году. Он заключается в уменьшении электрического сопротивления ${\displaystyle R}$ проводника конечных размеров с повышением его температуры ${\displaystyle T}$ (то есть ситуация ${\displaystyle dR/dT<0}$ для определённого температурного интервала). Эффект Гуржи обычно рассматривается как доказательство гидродинамического транспорта[3][4][5][6][7][8] в проводящих средах.

Эффект Гуржи
Названо в честь	Гуржи Радий Николаевич
Дата открытия	1963
Описывающая закон или теорему формула	${\displaystyle R\propto l_{ee}(T)/d^{2}\propto T^{-5}d^{-2}}$

Показаны разные режимы транспорта зарядов. Голубой круг — это электрон, движущийся в проводнике шириной d. Красные звезды соответствуют столкновениям с потерей полного импульса электрона. .

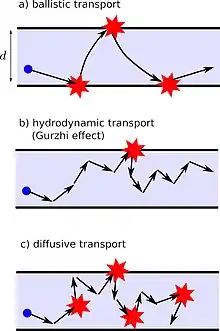
Механизм эффекта Гуржи следующий: Величина сопротивления проводника обратна ${\displaystyle l_{lost}=\min\{l_{boundary},l_{V}\}}$ — средняя длина свободного пробега, соответствующая потере импульса в системе электронов.

$${\displaystyle R\propto {\frac {1}{l_{lost}}},}$$

где ${\displaystyle l_{boundary}}$ — среднее расстояние, которое проходит электрон между двумя последовательными взаимодействиями с границей, ${\displaystyle l_{V}}$ — средняя длина свободного пробега, отвечающая другим возможностям потери импульса. Отражение электронов от границы считается диффузным.

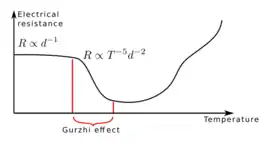
При низких температурах реализуется баллистический транспорт: ${\displaystyle l_{ee}\gg d}$, ${\displaystyle l_{lost}\approx l_{boundary}\approx d}$, где ${\displaystyle d}$ — ширина проводника, ${\displaystyle l_{ee}}$ — средняя длина свободного пробега, соответствующая нормальным электрон — электронным столкновениям (то есть столкновениям без процессов переброса импульса). При низких температурах фонон, излучаемый электроном, быстро взаимодействует с другим электроном без потери суммарного импульса электрон — фононной системы. ${\displaystyle l_{ee}\approx l_{ep}}$, где ${\displaystyle l_{ep}\propto T^{-5}}$ — средняя длина свободного пробега, соответствующая электрон — фононным столкновениям. Также предполагается ${\displaystyle d\ll l_{V}}$. Таким образом, сопротивление для самых низких температур является постоянным ${\displaystyle R\propto d^{-1}}$ (см. рисунок). Эффект Гуржи появляется при повышении температуры, когда длина пробега относительно электрон — электронных столкновений становится достаточно малой ${\displaystyle l_{ee}\ll d}$ . В этом режиме диффузионную длину пробега электронов между двумя последовательными взаимодействиями с границей можно рассматривать, как свободный пробег относительно потери импульса. Пользуясь известными формулами броуновского движения, легко показать, что длина траектории между двумя столкновениями с границей порядка ${\displaystyle l_{lost}\approx l_{boundary}\approx d^{2}/l_{ee}}$, а сопротивление пропорционально ${\displaystyle R\propto l_{ee}(T)/d^{2}\propto T^{-5}d^{-2}}$ . Таким образом, имеем отрицательную производную ${\displaystyle dR/dT<0}$ . Эффект Гуржи можно наблюдать при ${\displaystyle l_{ee}\ll d\ll d^{2}/l_{ee}\ll l_{V}}$ .

Эффект Гуржи отвечает необычной ситуации, когда электрическое сопротивление зависит от частоты нормальных столкновений. Этот эффект возникает из-за наличия границ образца, имеющего конечный характерный размер ${\displaystyle d}$ . Позже группа Гуржи обнаружила особую роль гидродинамики электронов в спиновом транспорте.[9][10] В этом случае магнитная неоднородность играет роль «границы» со спин — диффузионной длиной,[11] как характерным размером вместо ${\displaystyle d}$, как раньше. Эта магнитная неоднородность останавливает электроны одного направления и становится эффективным рассеивателем для электронов с противоположным спином. В этом случае магнетосопротивление проводника зависит от частоты нормальных электрон — электронных столкновений, а также от эффекта Гуржи.