Флаговый комплекс
Флаговый комплекс — симплициальный комплекс, в котором любой набор вершин, попарно соединённых рёбрами, образует симплекс.
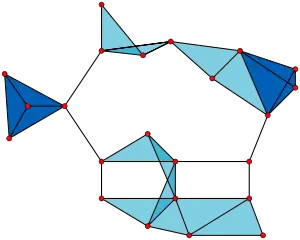
Пример флагового комплекса
Примеры
- -угольник является флаговым комплексом тогда и только тогда, когда .
- Естественное замощение сферы симплексами Коксетера является флаговой триангуляцией.
- Барицентрическое подразделение любого клеточного комплекса является флаговым.
- В частности, барицентрическое подразбиение симплициального комплекса является флаговым.
Свойства
- Флаговый комплекс полностью определяется своим одномерным остовом, то есть графом из вершин и рёбер комплекса.
- Более того, по любому графу можно построить флаговый комплекс, объявив, что каждая клика его вершин образует симплекс
- Линк любого симплекса флагового комплекса флаговый.
- Любой флаговый комплекс удовлетворяет следующему условию на треугольники:
- Если три вершины соединены рёбрами, то они образуют треугольник в комплексе.
- Более того, если симплициальный комплекс и все его линки удовлетворяют этому условию на треугольники, то он является флаговым.
- (критерий Громова) Предположим, симплициальный комплекс оснащён внутренней метрикой, такой, что каждый симплекс изометричен симплексу в единичной сфере со всеми углами прямыми. Полученное метрическое пространство является CAT(1) тогда и только тогда, когда комплекс является флаговым.
Ссылки
- Bandelt, H.-J. & Chepoi, V. (2008), Metric graph theory and geometry: a survey, in Goodman, J. E.; Pach, J. & Pollack, R., Surveys on Discrete and Computational Geometry: Twenty Years Later, vol. 453, Contemporary Mathematics, Providence, RI: AMS, с. 49–86, <http://pageperso.lif.univ-mrs.fr/~victor.chepoi/survey_cm_bis.pdf>.
- Berge, C. (1989), Hypergraphs: Combinatorics of Finite Sets, North-Holland, ISBN 0-444-87489-5.
- Chatterji, I. & Niblo, G. (2005), From wall spaces to CAT(0) cube complexes, International Journal of Algebra and Computation Т. 15 (5–6): 875–885, DOI 10.1142/S0218196705002669.
- Davis, M. W. (2002), Nonpositive curvature and reflection groups, in Daverman, R. J. & Sher, R. B., Handbook of Geometric Topology, Elsevier, с. 373–422.
- Dong, X. & Wachs, M. L. (2002), Combinatorial Laplacian of the matching complex, Electronic Journal of Combinatorics Т. 9: R17, <http://www.combinatorics.org/Volume_9/Abstracts/v9i1r17.html>.
- Hartsfeld, N. & Ringel, Gerhard (1991), Clean triangulations, Combinatorica Т. 11 (2): 145–155, DOI 10.1007/BF01206358.
- Hodkinson, I. & Otto, M. (2003), Finite conformal hypergraph covers and Gaifman cliques in finite structures, The Bulletin of Symbolic Logic Т. 9 (3): 387–405, DOI 10.2178/bsl/1058448678.
- Larrión, F.; Neumann-Lara, V. & Pizaña, M. A. (2002), Whitney triangulations, local girth and iterated clique graphs, Discrete Mathematics Т. 258: 123–135, doi:10.1016/S0012-365X(02)00266-2, <http://xamanek.izt.uam.mx/map/papers/cuello10_DM.ps>.
- Malnič, A. & Mohar, B. (1992), Generating locally cyclic triangulations of surfaces, Journal of Combinatorial Theory, Series B Т. 56 (2): 147–164, DOI 10.1016/0095-8956(92)90015-.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.