Упаковка квадратов в квадрате

5 единичных квадратов в квадрате со стороной ${\displaystyle 2+1/{\sqrt {2}}\approx 2.707}$

10 единичных квадратов в квадрате с длиной стороны ${\displaystyle 3+1/{\sqrt {2}}\approx 3.707}$

Для малого числа единичных квадратов ${\displaystyle n<100}$ оптимальные решения найдены для случаев ${\displaystyle n=1-10}$, ${\displaystyle 14-16}$, ${\displaystyle 23-25}$, ${\displaystyle 34-36}$, ${\displaystyle 46-49}$, ${\displaystyle 62-64}$, ${\displaystyle 79-81}$, ${\displaystyle 98-100}$.[2]

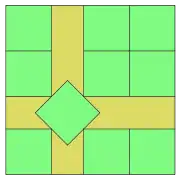
Если ${\displaystyle n}$ является полным квадратом, то наименьшее значение стороны квадратного контейнера ${\displaystyle a={\sqrt {n}}}$. Для оптимальных решений при малых ${\displaystyle n}$ , кроме случаев ${\displaystyle n=5}$ и ${\displaystyle n=10}$, упаковка представляет собой единичные квадраты, расположенные параллельно сторонам контейнера с размером ${\displaystyle a=\lceil {\sqrt {n}}\rceil }$. Для ${\displaystyle n=5}$ и ${\displaystyle n=10}$ оптимальной является упаковка, использующая повёрнутые квадраты (см. рисунки справа)[2]. Решение для ${\displaystyle n=5}$ дано Гёбелем [3] в 1979 году.

Оптимальность упаковки для ${\displaystyle n=7,8,15}$ впервые доказана Эль Мумни [4] в 1999 году, для ${\displaystyle n=6}$ — Керни и Шиу [5] в 2002 году, а в 2003 Стромквист [6] доказал оптимальность решения для ${\displaystyle n=10}$. В 2010 году Бентц [7] находит оптимальное решение для ${\displaystyle n=13}$ и ${\displaystyle n=46}$

Минимальным числом единичных квадратов, для которого на данный момент не найден оптимальный вариант упаковки, является ${\displaystyle 11}$. Для этого случая наилучшая упаковка предложенна Стромквистом[6]. Она дает размер стороны контейнера ${\displaystyle \textstyle a=2+2{\sqrt {4/5}}\approx 3,789}$.

В асимптотическом случае задача была сформулирована Эрдёшем и Грэмом в работе [1] следующим образом. Необходимо определить какое максимальное количество единичных квадратов ${\displaystyle n}$ может уместиться в большой квадратный контейнер со стороной размером ${\displaystyle a\rightarrow \infty }$. При решении этой задачи нужно минимизировать незанятое пространство, определенное в [1] как

${\displaystyle W(a)=a^{2}-sup\left\{|{\mathcal {P}}|\mid {\mathcal {P}}\right\}}$,

где ${\displaystyle {\mathcal {P}}}$ есть множество всех возможный упаковок единичных квадратов, а ${\displaystyle |{\mathcal {P}}|}$ есть количество единичных квадратов. Отметим, что в случае целочисленного ${\displaystyle a}$ получаем ${\displaystyle n=a^{2}}$ и ${\displaystyle W(a)=0}$.

В случае не целочисленного значения ${\displaystyle a}$ и «наивной» упаковки в виде рядов единичных квадратов, параллельных стенам контейнера, у незанятого пространства наблюдается линейный рост относительно ${\displaystyle a}$ [8]:

${\displaystyle W(a)\sim a(a-\lfloor a\rfloor )}$ .

Эрдёш и Грэм показали [1], что существует упаковка, дающая существенно нелинейную зависимость незанятого пространства от размера контейнера ${\displaystyle W(a)\sim O(a^{7/11})}$ (запись в терминах «O» большое), и выдвинули гипотезу, что асимптотическое поведение оптимальной упаковки ${\displaystyle W(a)\sim O(a^{1/2})}$ . Однако Рот и Воган в работе [9], для асимптотики из полуцелых значений ${\displaystyle a}$, получили ${\displaystyle W(a)>c{\sqrt {a}}}$ , где ${\displaystyle c}$ есть некая константа.

На данный момент наилучшей упаковкой в асимптотическом случае является упаковка, предложенная Грэмом и Чоном в работе [8] с асимптотикой ${\displaystyle W(a)\sim O(a^{3/5})}$, а точная асимптотическая скорость роста незаполненного пространства остаётся открытой проблемой

• Упаковка окружностей в квадрат
• Квадрирование квадрата