Точка Понселе
Точка Понселе — предмет следующей теоремы[1]:
|
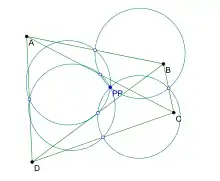
Замечание
- В теореме Понселе выше речь идет о системе 4 точек, не являющихся так называемой ортоцентрической системой 4 точек.
- Если в четвёрке точек , , , точка является точкой пересечения высот треугольника , то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек. Другие свойства ортоцентрической системы точек см. в статье ортоцентр.
- В определении выше для точки Понселе можно отказаться от упоминания ортоцентрической системы точек, если, например, заменить его системой 4 точек, образующих вершины выпуклого невырожденного четырехугольника, которые автоматически никогда не образуют ортоцентрическую систему точек.
- Кстати, если в определении выше для точки Понселе система 4 точек все-таки окажется ортоцентрической, то точка Понселе станет просто окружностью Эйлера (бесконечным множеством точек), общей для ортоцентрической системы точек.
Свойства точки Понселе
Если — ортоцентр треугольника , то точки Понселе для четвёрок точек , , , совпадают.
Точка Понселе четвёрки точек лежит на педальной окружности точки относительно треугольника , то есть на описанной окружности подерного треугольника точки относительно треугольника .
Точка Понселе четвёрки точек является центром равнобокой гиперболы, проходящей через точки , , , .
Точка Понселе четвёрки точек лежит на чевианной окружности точки относительно треугольника , то есть на окружности, содержащей основания чевиан треугольника , проходящих через точку .
Точка Понселе четвёрки является серединой отрезка, соединяющего точки и , где - образ точки при антигональном сопряжении относительно треугольника
Точки Понселе четвёрок и совпадают.
Замечание
- Антигональное сопряжение - тоже что и анти изогональное сопряжение.[2]
Литература
- Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду / Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова.. — Москва: МЦНМО, 2009. — ISBN 978-5-94057-477-4.
- Vonk, Jan (2009), The Feuerbach point and reflections of the Euler line, Forum Geometricorum Т. 9: 47–55, <http://forumgeom.fau.edu/FG2009volume9/FG2009Volume9.pdf#page=51>
См. также
Примечания
- Заславский, Пермякова и др., 2009, с. 118, задача 9.
- См. Антигональное сопряжение // http://yavix.ru/%D0%B2%D0%B8%D0%BA%D0%B8%20%D0%9A%D0%BE%D0%BB%D0%BB%D0%B8%D0%BD%D0%B5%D0%B0%D1%80%D0%BD%D1%8B%D0%B5%20%D1%82%D0%BE%D1%87%D0%BA%D0%B8