Точка Парри

Окружность и точка Парри. (G — центроид, а J и K являются точками Аполлония треугольника ABC)

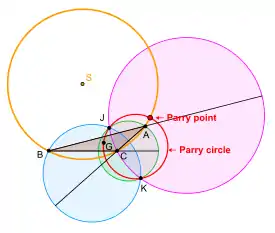
Пусть ABC — треугольник на плоскости. Окружность, проходящая через центроид и две точки Аполлония треугольника ABC, называется окружностью Парри треугольника ABC. Уравнением окружности Парри в трилинейных координатах является[2]

${\displaystyle {\begin{aligned}&3(b^{2}-c^{2})(c^{2}-a^{2})(a^{2}-b^{2})(a^{2}yz+b^{2}zx+c^{2}xy)\\[6pt]&{}+(x+y+z)\left(\sum _{\text{cyclic}}b^{2}c^{2}(b^{2}-c^{2})(b^{2}+c^{2}-2a^{2})x\right)=0\end{aligned}}}$

Центр окружности Парри также является замечательной точкой треугольника и перечислен под именем X(351) в Энциклопедии центров треугольника. Трилинейные координаты центра окружности Парри равны

f(a, b, c) : f (b , c, a) : f (c, a, b), где f (a , b, c) = a (b² − c²) (b² + c² − 2a²).

Окружность Парри и описанная окружность треугольника ABC пересекаются в двух точках. Одна из них — фокус параболы Киперта треугольника ABC[3]. Другая точка пересечения называется точкой Парри треугольника ABC.

Трилинейные координаты точки Парри равны

(a / (2 a² − b² − c²) : b / (2 b² − c² − a²) : c / (2 c² − a² − b²))

Точка пересечения окружности Парри и описанной окружности треугольника ABC, которая является фокусом гиперболы Киперта треугольника ABC, перечислена под именем X(110) в Энциклопедии центров треугольника. Трилинейные координаты этой точки

(a / (b² − c²) : b / (b² − a²) : c / (a² − b²))

• Окружность Лестера

• Clark Kimberling. Parry point. — 2012.
• Paul Yiu. The Circles of Lester, Evans, Parry, and Their Generalizations // Forum Geometricorum. — 2010. — Т. 10.