Теорема о совершенных графах

Совершенный граф — это неориентированный граф, в любом порождённом подграфе которого размер его наибольшей клики равен минимальному числу цветов раскраски подграфа. Совершенные графы включают много важных классов графов, куда входят двудольные графы, хордальные графы и графы сравнимости.

Дополнение графа имеет ребро между двумя вершинами тогда и только тогда, когда исходный граф такого ребра не имеет. Таким образом, клика в исходном графе становится независимым множеством в дополнении и раскраска исходного графа становится кликовым покрытием дополнения.

Теорема о совершенных графах утверждает:

Дополнение совершенного графа совершенно.

Эквивалентная формулировка: В совершенном графе размер наибольшего независимого множества равен минимальному числу клик в кликовом покрытии.

Цикл с семью вершинами и его дополнение, антидыра с семью вершинами. На рисунке показаны оптимальные раскраски и наибольшие клики (показаны жирными рёбрами). Поскольку в обоих графах число цветов не совпадает с размером клики, оба графа не являются совершенными.

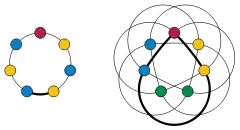
Пусть G — граф-цикл нечётной длины, большей трёх (так называемая «нечётная дыра»). Тогда требуется для любой раскраски G по меньшей мере три цвета, но нет ни одного треугольника, так что граф не совершенен. По теореме о совершенных графах, дополнение графа G («нечётная антидыра») должно поэтому также быть несовершенным. Если граф G является циклом из пяти вершин, он изоморфен своему дополнению, но это неверно для более длинных циклов. Нетривиальной задачей является вычисление кликового числа и хроматического числа в нечётной антидыре и нечётной дыре. Как утверждает строгая теорема о совершенных графах, нечётные дыры и нечётные антидыры оказываются минимальными запрещёнными порождёнными подграфами совершенных графов.

В нетривиальном двудольном графе оптимальное число цветов (по определению) равно двум, и (поскольку двудольные графы не содержат треугольников) наибольший размер клики равен также двум. Таким образом, любой порождённый подграф двудольного графа остаётся двудольным. Таким образом, двудольные графы являются совершенными. В двудольных графах с n вершинами наибольшее покрытие кликами принимает форму наибольшего паросочетания вместе с дополнительной кликой для каждой непокрытой вершины с размером n − M, где M — число элементов в паросочетании. В этом случае из теоремы о совершенных графах следует теорема Кёнига, что размер максимального независимого множества в двудольном графе в двудольном графе также равно n − M[6], результат, который был главным стимулом формулировки Бержем теории совершенных графов.

Теорему Мирского, описывающую высоту частично упорядоченного множества в терминах разбиения на антицепи, можно сформулировать как совершенство графа сравнимости частично упорядоченного множества, а теоремы Дилуорса, описывающие ширину частично упорядоченного множества в терминах разбиения на цепочки, можно сформулировать как совершенство дополнений этих графов. Таким образом, теорема о совершенном графе может быть использована для доказательства теоремы Дилуорса, опираясь на (более простое) доказательство теоремы Мирского, или наоборот[7].

Для доказательства теоремы о совершенных графах Ловаш использовал операцию замены вершин в графе кликами. Уже Бержу было известно, что если граф совершенен, полученный такой заменой граф также будет совершенным[8]. Любой такой процесс замены может быть разбит на повторяющиеся шаги дублирования вершин. Если дублируемая вершина принадлежит наибольшей клике графа, она увеличивает кликовое число и хроматическое число на единицу. Если, с другой стороны, дублируемая вершина не принадлежит наибольшей клике, образуем граф H путём удаления вершин того же цвета, что и у дублируемой (но не саму дублируемую вершину) из оптимальной раскраски графа. Удаляемые вершины входят во все наибольшие клики, так что H имеет число клик и хроматическое число на единицу меньше, чем в исходном графе. Удалённые вершины и новые копии задублированных вершин могут быть добавлены в единый класс цвета, что показывает, что шаг дублирования не меняет хроматическое число. Те же доводы показывают, что удвоение сохраняет равенство числа клик хроматическому числу в каждом порождённом подграфе данного графа, так что каждый шаг удвоения сохраняет совершенство графа[9].

Если задан совершенный граф G, Ловаш образует граф G* путём замены каждой вершины v кликой с t_v вершинами, где t_v является числом различных максимальных различных множеств в G, содержащих v. Можно сопоставить каждой из различных максимальных независимых множеств из G максимальное независимое множество в G* таким образом, что независимые множества в G* все не будут пересекаться и каждая вершина G* появляется в единственном выбранном множестве. То есть G* имеет раскраску, в которой каждый класс цвета является максимальным независимым множеством. Необходимым образом эта раскраска будет оптимальной раскраской G*. Поскольку G совершенен, таковым является и G*, а тогда он имеет максимальную клику K*, размер которой равен числу цветов в этой раскраске, что равно числу различных максимальных независимых множеств в G. Необходимым образом K* содержит различные представления для каждого из этих максимальных множеств. Соответствующее множество K вершин в G (вершин, расширенные клики которых в G* пересекают K*) является кликой в G со свойством, что оно пересекает любое максимальное независимое множество в G. Таким образом, граф, образованный из G путём удаления K, имеет число кликового покрытия, не превосходящее кликового числа графа G без единицы, а число независимости по меньшей мере на единицу меньше числа независимости графа G. Результат следует из индукции по этому числу [10]

Сильная теорема о совершенных графах Чудновской, Робертсона, Сеймура и Томаса[11] утверждает, что граф является совершенным тогда и только тогда, когда ни один из порождённых подграфов не является циклом нечётной длины, большей либо равной пяти, а также не является дополнением такого цикла. Поскольку такое описание нечувствительно к операции дополнения графа, отсюда немедленно следует слабая теорема о совершенных графах.

Камерон, Эдмондс и Ловаш [12] доказали, что если рёбра полного графа разбиты на три подграфа таким образом, что любые три вершины порождают связный граф в одном из трёх подграфов, и если два из подграфов совершенны, то третий подграф тоже совершенный. Теорема о совершенном графе является частным случаем этого результата, когда один из трёх графов является пустым графом.