Теорема об опорной гиперплоскости

Прямоугольный треугольник ${\displaystyle \triangle c'c^{*}z^{*}}$

Пусть ${\displaystyle d(c,\;z^{*})}$ − расстояние между точкой ${\displaystyle z^{*}}$ и точкой ${\displaystyle c\in C}$. Так как множество ${\displaystyle C}$ замкнуто и ограничено, то, оно и компактно, а поскольку функция расстояния ${\displaystyle d(c,\;z^{*})}$ непрерывна, то она достигает своего минимума в некоторой точке ${\displaystyle c^{*}\in C}$.

Пусть ${\displaystyle P}$ − гиперплоскость, проходящая через точку ${\displaystyle z^{*}}$, перпендикулярная прямой, соединяющей точки ${\displaystyle c^{*}}$ и ${\displaystyle z^{*}}$.

Докажем, что ни одна из точек множества ${\displaystyle C}$ не содержится в гиперплоскости ${\displaystyle P}$.

Предположим обратное, что существует некоторая точка ${\displaystyle c'}$, принадлежащая, как множеству ${\displaystyle C}$, так и гиперплоскости ${\displaystyle P}$.

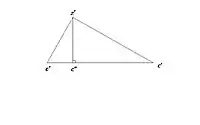
Тогда в двухмерной плоскости, являющейся линейной оболочкой точек ${\displaystyle c',z^{*},c^{*}}$, эти точки образуют прямоугольный треугольник

${\displaystyle \triangle c'c^{*}z^{*}}$ с прямым углом в вершине ${\displaystyle z^{*}}$.

При этом любая точка ${\displaystyle c''}$ отрезка ${\displaystyle c',c^{*}}$ является выпуклой комбинацией точек ${\displaystyle c',c^{*}\in C}$ и потому принадлежит ${\displaystyle C}$. Однако, если в качестве ${\displaystyle c''}$, взять основание перпендикуляра, опущенного из вершины ${\displaystyle z^{*}}$ на гипотенузу ${\displaystyle c^{*}c'}$, то расстояние от точки ${\displaystyle c''}$ до вершины ${\displaystyle z^{*}}$ будет строго меньше, чем расстояние от вершины ${\displaystyle z^{*}}$ до вершины ${\displaystyle c^{*}}$, т.е.

${\displaystyle d(c'',\;z^{*})<d(c^{*},\;z^{*})}$.

Следовательно точка ${\displaystyle c'}$ не может принадлежать множеству ${\displaystyle C}$, так как это предположение противоречит тому, что функция ${\displaystyle d(c,\;z^{*})}$ достигает своего минимума в точке ${\displaystyle c^{*}}$.

Таким образом, ни одна из точек множества ${\displaystyle C}$ не содержится в гиперплоскости ${\displaystyle P}$. Значит, всё множество ${\displaystyle C}$ содержится в одном из двух полупространств, определяемых

гиперплоскостью ${\displaystyle P}$. Эти полупространства определяются следующими неравенствами:

${\displaystyle a_{1}z_{1}+a_{2}z_{2}+...+a_{m}z_{m}>b}$

и

${\displaystyle a_{1}z_{1}+a_{2}z_{2}+...+a_{m}z_{m}<b}$,

где числа ${\displaystyle a_{i}(1\leqslant i\leqslant m)}$ и ${\displaystyle b}$ являются коэффициентами уравнения гиперплоскости ${\displaystyle P}$, задаваемой уравнением:

${\displaystyle a_{1}z_{1}+a_{2}z_{2}+...+a_{m}z_{m}=b}$

Теперь, если заменить ${\displaystyle a_{1},a_{2},...,a_{m},b}$ на ${\displaystyle -a_{1},-a_{2},...,-a_{m},-b}$, т.е. умножить уравнение гиперплоскости ${\displaystyle P}$ на ${\displaystyle -1}$, то гиперплоскость останется неизменной, а полупространства поменяются местами. Следовательно, можно считать, что полупространство, в котором содержится множество ${\displaystyle C}$, определяется неравенством:

${\displaystyle a_{1}z_{1}+a_{2}z_{2}+...+a_{m}z_{m}>b}$.

Это доказывает теорему.

• Дж. фон Нейман. Теория игр и экономическое поведение / Дж. фон Нейман, О. Моргенштерн. Пер. с англ. под ред. и с доб. Н.Н. Воробьева. - М. : Наука. Главная редакция физико-математической литературы, 1970. - 708 с.
• Дюбин, Г.Н. Введение в прикладную теорию игр / Г.Н. Дюбин, В.Г. Суздаль. – М. : Наука. Главная редакция физико-математической литературы, 1981. – 336 с.
• Оуэн, Г. Теория игр. / Г. Оуэн. [пер. с англ.] / Под ред. А.А. Корбута. – М. : Издательство «Мир», 1971. – 229 с.