Теорема Робертса о треугольниках
Теорема Робертса о треугольниках утверждает, что среди кусков, на которые прямых в общем положении разрезают плоскость, найдётся хотя бы треугольника.
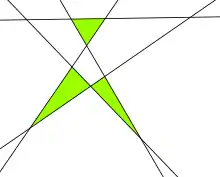
конфигурация из пяти прямых с тремя треугольниками.
Теорема знаменита простой формулировкой и большим числом ошибочных решений. В частности, Робертс, именем которого названа теорема, дал ошибочное доказательство. Эта задача была решена Шенноном только спустя 90 лет с момента постановки.
Формулировка
Пусть на плоскости даны прямых в общем положении, то есть никакие две не параллельны и никакие три не пересекаются в одной точке. Тогда среди многоугольных областей, на которые эти прямые разрезают плоскость, найдётся хотя бы треугольника.
История
- Вопрос был сформулирован и решён Робертсом в 1889 году.
- В 1972 году Бранко Грюнбаум указал на ошибку в доказательстве.
- В 1979 году Шеннон дал первое доказательство теоремы.
- В начале 1980-х задача стала популярна в математических кружках СССР.
- В 1985 году изящное элементарное доказательство, использующее линейную алгебру, дал Алексей Канель-Белов, оно было опубликовано только в 1992.
- В 1998 году простое чисто комбинаторное доказательство было представлено Штефаном Фелснером и Клаусом Кригелом
- Их доказательство работает также для конфигураций псевдопрямых.
О доказательствах
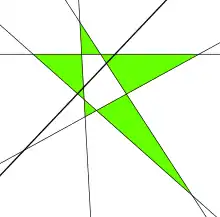
Конфигурация из пяти прямых в которой добавление шестой не увеличивает число треугольников.
- Стандартная ошибка заключается в попытке доказать, что при добавление одной прямой к конфигурации увеличивает число треугольников хотя бы на 1, и таким образом доказать теорему индукцией по . Легко доказать, что добавление одной прямой не уменьшает числа треугольников, однако оно не всегда добавляет 1 к их числу.
- Идея Канеля-Белова состоит в следующем. Если число треугольников меньше , то по стандартному рассуждению линейной алгебры можно закрепить две прямые и двигать остальные параллельно так, что периметры всех треугольников остаются одинаковыми. При таком движении новых треугольников не образуется, и старые не могут «умереть». Используя такое движение, можно привести конфигурацию прямых к более простому случаю, в котором доказательство несложно.
- Идея Фелснерa и Кригелa состоит в следующем. В каждом куске разбиения посадим по цветку на каждую сторону, при которой сумма смежных с ней углов . Заметим что на каждую сторону посажен ровно один цветок, отсюда число цветков равно . Далее в заметим, что в каждом треугольнике ровно три цветка, а в ограниченном многоугольнике, отличном от треугольника, не больше двух цветков. Индукцией по получаем, что число ограниченных многоугольников разбиения равно
- .
- Значит, если число треугольников обозначить за , получаем
- ,
- откуда немедленно следует желанное .
Вариации и обобщения
- Утверждение остаётся верным если в конфигурации прямых нет параллельных и не все прямые проходят через одну точку.
- Аналогичная задача на проективной плоскости проще, прямых вырезают хотя бы треугольников. Эта оценка точная при . Доказательство было дано Фридрихом Леви в 1926 году, оно основано на том, что каждая прямая граничит хотя бы с тремя треугольниками.
- Среди кусков -мерного евклидова пространства, на которые его разбивают гиперплоскостей в общем положении, найдётся хотя бы симплексов.
Литература
- А. Канель, А. Ковальджи. Треугольники и катастрофы // Квант. — 1992. — № 11. — С. 42—50.
- А. Я. Белов. Об одной задаче комбинаторной геометрии // УМН. — 1992. — Т. 47, № 3(285). — С. 151–152.
- B. Grünbaum. How many triangles? (англ.) // Geombinatorics. — 1998. — Vol. 8, no. 1. — P. 154—159.
- B. Grünbaum. Arrangements and spreads (англ.). — 1972. — iv+114 p.
- S. Felsner, K. Kriegel. Triangles in Euclidean arrangements (англ.) // Discrete Comput. Geom.. — 1999. — Vol. 22, no. 3. — P. 429—438.
- F. Levi. Die Teilung der projektiven Ebene durch Gerade oder Pseudogerade (нем.) // Ber. Math.-Phys. Kl. Sächs. Akad. Wiss. — 1926. — Bd. 78. — S. 256—267.
- S. Roberts. On the figures formed by the intercepts of a system of straight lines in the plane and on analogous relations in space of three dimensions (англ.) // Proc. London Math. Soc.. — 1889. — Vol. 19. — P. 405–422.
- R. W. Shannon. Simplicial cells in arrangements of hyperplanes (англ.) // Geom. Dedicata. — 1979. — Vol. 8. — P. 179–187.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.