Теорема Неймана-Моргенштерна о минимаксе

В теории игр, теорема о минимаксе описывает условия, при выполнении которых для функции $f:Z\times W\to \mathbb {R}$ верно, что $\sup _{x\in Z}\inf _{y\in W}f=\inf _{y\in Z}\sup _{x\in W}f.$ Первой теоремой такого рода стала теорема фон Неймана, доказанная в 1928 году. Именно с её доказательства началось развитие теории игр. Впоследствии её неоднократно обобщали и переформулировали. [1][2]

Игры с нулевой суммой

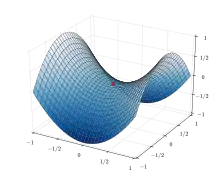
Функция f(x,y)=x²-y² выпукла по

x

, но вогнута по

y

Эту теорему впервые доказал в 1928 году Джон фон Нейман[3] [4]

Формально, теорема фон Неймана утверждает, что

Пусть $X\subset \mathbb {R} ^{n}$ и $Y\subset \mathbb {R} ^{m}$ ― компактные выпуклые множества. Если функция $f:X\times Y\rightarrow \mathbb {R}$ непрерывна, выпукла в $X$ , но вогнута в $Y$ , т.е.

f(\cdot ,y):X\rightarrow \mathbb {R}

выпукла при любом заданном

y

, но

f(x,\cdot ):Y\rightarrow \mathbb {R}

вогнута при любом заданном

x

,

то

\max _{x\in X}\min _{y\in Y}f(x,y)=\min _{y\in Y}\max _{x\in X}f(x,y).

Примеры

Если $f(x,y)=x^{T}Ay$ для конечной матрицы $A\in \mathbb {R} ^{n\times m}$ , то $\max _{x\in X}\min _{y\in Y}x^{T}Ay=\min _{y\in Y}\max _{x\in X}x^{T}Ay.$

См. также

Теорема Сиона о минимаксе
Теорема Партасавати, являющаяся обобщением теоремы о минимаксе
Двойственная задача линейного программирования, облегчающая поиск оптимальных стратегий в играх с нулевой суммой
Принцип Яо

Примечания

Minimax and Applications. — Boston, MA : Springer US, 1995. — ISBN 9781461335573.
Brandt, Felix; Brill, Markus; Suksompong, Warut (2016). “An ordinal minimax theorem”. Games and Economic Behavior. 95: 107—112. arXiv:1412.4198. DOI:10.1016/j.geb.2015.12.010.
Von Neumann, J. (1928). “Zur Theorie der Gesellschaftsspiele”. Math. Ann. 100: 295—320. DOI:10.1007/BF01448847.
John L Casti. Five golden rules: great theories of 20th-century mathematics – and why they matter. — New York : Wiley-Interscience, 1996. — P. 19. — ISBN 978-0-471-00261-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Minimax and Applications. — Boston, MA : Springer US, 1995. — ISBN 9781461335573.

[2] Brandt, Felix; Brill, Markus; Suksompong, Warut (2016). “An ordinal minimax theorem”. Games and Economic Behavior. 95: 107—112. arXiv:1412.4198. DOI:10.1016/j.geb.2015.12.010.

[3] Von Neumann, J. (1928). “Zur Theorie der Gesellschaftsspiele”. Math. Ann. 100: 295—320. DOI:10.1007/BF01448847.

[Casti-4] John L Casti. Five golden rules: great theories of 20th-century mathematics – and why they matter. — New York : Wiley-Interscience, 1996. — P. 19. — ISBN 978-0-471-00261-1.