Теорема Гамильтона
Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
.png.webp)
Пример
Если на показанном рисунке ортоцентр остроугольного треугольника ABC обозначить через T, тогда три треугольника Гамильтона TAB, TBC и TCA имеют общую окружность Эйлера (окружность девяти точек).
Ассоциация
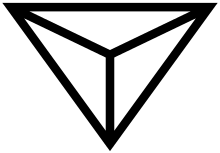
Три треугольника Гамильтона в теореме Гамильтона образуют так называемый глаз дракона.
Применение
Теорема Гамильтона используется, как составная часть, в теореме Джонсона (см. рисунок).

Следствия
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника. Назовем их окружностями Гамильтона-Джонсона
- Радиусы описанных окружностей трёх треугольников Гамильтона имеют три центра JA, JB и JC. Эти три центра образуют вершины треугольника Джонсона ΔJAJBJC , который равен исходному треугольнику Δ ABC и имеет попарно параллельные с ним стороны (Теорема Джонсона, см. рисунок).
- Если через вершины исходного треугольника ABC провести прямые, параллельные противоположным сторонам, то получится антидополнительный треугольник, подобный исходному треугольнику ABC, вершины которого PA, PB и PC лежат на трёх окружностях Гамильтона-Джонсона, имеющих равные радиусы (см. рис.).
Замечание 1
Оба следствия немедленно следуют из теоремы Гамильтона, если заметить, что радиус окружности Эйлера равен половине радиуса окружности, описанной около того же треугольника.
Замечание 2
- Для тупоугольного треугольника теорема Гамильтона переформулируется следующим образом. Пусть вне тупоугольного треугольника постороили ортоцентр, как точку пресечения двух его высот, опущенных из вершин двух острых углов на продолжения двух его сторон, и продолжения третьей высоты, проведённой из вершины тупого угла. Тогда ортоцентр и две вершины острых углов образуют остроугольный треугольник, к которому применима теорема Гамильтона. В частности, сам тупоугольный треугольник будет одним из трёх треугольников Гамильтона. Вершинами двух других треугольников Гамильтона служат ортоцентр и вершины двух смежных сторон, образующих тупой угол тупоугольного треугольника.
- Для прямоугольного треугольника ортоцентр совпадает с вершиной прямого угла, и один треугольник Гамильтона совпадает с самим этим прямоугольным треугольником c верным радиусом (диаметром) описанной окружности. Остальные два треугольника Гамильтона вырождаются в два катета при вершине прямого угла. Через эти два катета (как через треугольник с двумя точками — вершинами) можно провести бесчисленное множество описанных окружностей с диаметрами не меньше длины этих катетов. То есть теорема Гамильтона формально выполняется и в этом предельном случае.
Пример
Если на показанном рисунке ортоцентр остроугольного треугольника ABC обозначить через T, тогда для тупоугольного треугольника TBC ортоцентром будет точка A. Перейдя от тупоугольного треугольника TBC к остроугольному треугольнику ABC, снова можно использовать теорему Гамильтона.
История
Теорема была доказана выдающимся ирландским математиком и физиком XIX века Уильямом (Вильямом) Роуэном Гамильтоном в 1861 г. Гамильтон, Уильям Роуэн (1806—1865) — ирландский математик.
Литература
- Дм. Ефремов. Новая геометрия треугольника. — 1902. Архивная копия от 2 марта 2005 на Wayback Machine
- Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — 153 с.
- Уильям Роуэн Гамильтон http://free-math.ru/publ/istorija_matematiki/velikie_matematiki/gamilton_uiljam_rouehn/22-1-0-168