Суперэллипсоид
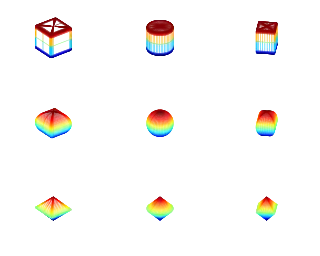
Суперэллипсоид — геометрическое тело, поперечными сечениями которого являются суперэллипсы (кривые Ламе) с одним и тем же показателем степени r, а вертикальные сечения — суперэллипсы с одним и тем же показателем степени t[1][2]. Некоторые суперэллипсоиды являются суперквадриками, однако ни одно из этих семейств не является подмножеством другого.
Частным случаем суперэллипсоида является суперъяйцо, популяризованное Питом Хейном.
Математическое описание
Базовая форма
Базовый суперэллипсоид определяется уравнением
Параметры r и t — положительные действительные числа, которые определяют форму фигуры, в частности — степень плоскостности полюсов и экватора. Когда t = r, суперэллипс становится частным случаем суперквадрики.
Любая параллель (горизонтальное сечение) суперэллипсоида плоскостью z = b, где -1 < b < +1, является кривой Ламе с показателем степени r, и масштабным коэффициентом
Любой меридиан (сечение плоскостью, проходящей через ось симметрии) также является кривой Ламе с показателем степени t и вытянутой в горизонтальном направлении с коэффициентом w, зависящим от положения секущей плоскости. Именно, если x = u cos θ и y = u sin θ при фиксированном θ, то
где
В частности, если r = 2, горизонтальные сечения являются кругами, а w = 1 для всех секущих плоскостей. В этом случае суперэллипсоид является телом вращения, полученной вращением кривой Ламе с показателем степени t вокруг вертикальной оси.
Базовый суперэллипсоид располагается в пространстве внутри куба, где значения каждой из трёх координат лежат в пределах от −1 до +1. Суперэллипсоид общего вида получается масштабированием базового суперэллипсоида по координатным осям с коэффициентамиA, B, C, которые являются полуосями получившегося суперэллипсоида. Уравнение суперэллипсоида общего вида
Принимая r = 2, t = 2,5, A = B = 3, C = 4, получим суперъяйцо Пита Хейна.
Суперэллипсоид общего вида представляется в параметрическом виде через параметры u and v (долгота и широта)[2]:
где
Объём суперэллипсоида выражается формулой
Примечания
- Barr, A.H. (January 1981), Superquadrics and Angle-Preserving Transformations. IEEE_CGA vol. 1 no. 1, pp. 11–23
- Barr, A.H. (1992), Rigid Physically Based Superquadrics. Chapter III.8 of Graphics Gems III, edited by D. Kirk, pp. 137–159
См. также
Ссылки
- Jaklič, A., Leonardis, A., Solina, F., Segmentation and Recovery of Superquadrics. Kluwer Academic Publishers, Dordrecht, 2000.
- Bibliography: SuperQuadric Representations
- Superquadric Tensor Glyphs Архивная копия от 4 февраля 2012 на Wayback Machine
- SuperQuadric Ellipsoids and Toroids, OpenGL Lighting, and Timing
- Superquadratics by Robert Kragler, The Wolfram Demonstrations Project.