Стандартное отображение
Стандартное отображение (англ. Standard map), известное также как стандартное отображение Чирикова (англ. Chirikov standard map) и отображение Чирикова — Тейлора (англ. Chirikov-Taylor map) — нелинейное отображение (сохраняющее объём) для двух канонических переменных, (импульса и координаты). Отображение известно своими хаотическими свойствами, которые впервые были исследованы[1] Борисом Чириковым в 1969 году.
Отображение задается такими итерационными уравнениями:
где параметр контролирует хаотичность системы.
Модель ротатора
Стандартное отображение описывает движение классического ротатора — фиксированного стержня, на который не действует сила тяжести и который вращается без трения в плоскости вокруг оси, проходящей через один из его концов. Ротатор также испытывает вызванные внешней силой периодические во времени (с периодом единица) удары бесконечно короткой продолжительности. Переменные и соответствуют углу поворота ротатора и его угловому моменту после -го удара. Параметр описывает силу удара. Функция Гамильтона ротатора может быть записана так:
где функция — периодическая функция с периодом 1, на одном периоде совпадает с δ-функцией Дирака. Из вышеприведенной функции Гамильтона элементарно получается стандартное отображение.
Свойства
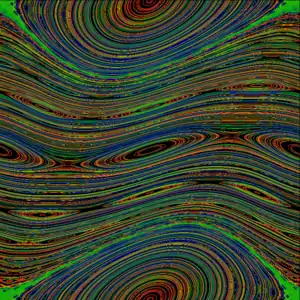


Для случая отображение является линейным, поэтому существуют лишь периодические и квазипериодические траектории. При отображение становится нелинейным, согласно теореме КАМ, происходит разрушение инвариантных торов и движения стохастических слоев, в которых динамика является хаотической. Рост приводит к увеличению областей хаоса на фазовой плоскости . Благодаря периодичности функции , динамику системы можно рассматривать на цилиндре [взяв ] или на торе [взяв ].
Стационарные точки отображения определяются из условия . На интервале , такими точками являются и (вследствие симметричности фазовой плоскости системы при инверсии относительно точки стационарные точки и можно не рассматривать).
Анализ линейной устойчивости отображения сводится к анализу системы уравнений
Из условия можно определить собственные значения матрицы для обоих стационарных точек [ и ]:
Поскольку , то отсюда следует неравенство . В то же время справедливо неравенство для произвольных . Таким образом стационарная точка является неустойчивой гиперболической точкой. Стационарная точка является устойчивой эллиптической точкой при , поскольку тогда . Для стационарная точка теряет устойчивость и становится гиперболической.
Ниже критического значения параметра, (рис. 1) инвариантные торы делят фазовое пространство системы так, что момент импульса является ограниченным — иными словами, диффузия в стохастическом слое не может выходить за границы, ограниченные инвариантными торами. «Золотой» инвариантный тор разрушается, когда число вращения достигает значения , что соответствует критическому значению параметра (фазовое пространство системы для изображено на рис. 2). На данный момент строго не доказано, что , однако численные расчеты показывают, что это скорее всего так. На сегодняшний день существует лишь строгое доказательство того, что при наблюдается режим глобального хаоса, когда стохастическое море с отдельными островками устойчивости покрывает всё фазовое пространство (см. рис. 3). Инвариантных торов, ограничивающих эволюцию в фазовом пространстве, уже нет, и можно говорить о диффузии траектории в хаотическом море.
Энтропия Колмогорова — Синая стандартного отображения хорошо описывается соотношением для значений контрольного параметра [2]
Квантовое стандартное отображение
Переход на квантового стандартного отображения происходит заменой динамических переменных квантовомеханическими операторами , которые удовлетворяют коммутационному соотношению , где — эффективная безразмерная постоянная Планка.
Основным свойством квантового отображения по сравнению с классическим является так называемое явление динамической локализации, заключающейся в подавлении хаотической диффузии за счёт квантовых эффектов[3].
Применение
Много физических систем и явлений сводятся к стандартному отображению. Это, в частности,
- динамика частиц в ускорителях;
- динамика кометы в Солнечной системе;
- микроволновая ионизация ридберговских атомов и автоионизация молекулярных ридберговских состояний;
- электронный магнетотранспорт в резонансном туннельном диоде;
- удержание заряженных частиц в зеркальных магнитных ловушках.
Модель Френкеля — Конторовой
Модель Френкеля — Конторовой следует выделить отдельно как первую модель, в которой уравнения стандартного отображения были записаны аналитически. Эта модель используется для описания динамики дислокаций, монослоев на поверхностях кристаллов, волн плотности заряда, сухого трения. Модель в стационарном случае задаёт связь между положениями взаимодействующих частиц (например, атомов) в поле пространственно-периодического потенциала. Функция Гамильтона одномерной цепочки атомов, взаимодействующих с ближайшими соседями через параболический потенциал взаимодействия и находящимися в поле косинусоидального потенциала, который описывает кристаллическую поверхность, имеет следующий вид:
Здесь — отклонение атома от своего положения равновесия. В стационарном случае () это приводит к следующему уравнению
которое заменой можно свести к обычной записи стандартного отображения.
Примечания
- Chirikov B. V. Research concerning the theory of nonlinear resonance and stochasticity // Preprint N 267, Institute of Nuclear Physics, Novosibirsk (1969), (Engl. Trans., CERN Trans. 71-40 (1971)).
- Chirikov B. V. A universal instability of many-dimensional oscillator systems // Phys. Rep. 52: 263 (1979).
- Casati G., Chirikov B. V., Izrailev F. M., Ford J. Lecture Notes in Physics — Berlin: Springer, 93: 334 (1979).
Литература
- Стандартное отображение Чирикова на www.scholarpedia.org (англ.).
- Weisstein, Eric W. Standard map (англ.) на сайте Wolfram MathWorld.
- Lichtenberg, A. J. and Lieberman, M. A. Regular and Chaotic Dynamics (неопр.). — Springer, Berlin, 1992..
- Ott, Edward. Chaos in Dynamical Systems (неопр.). — Cambridge University Press New, York, 2002..
- Sprott, Julien Clinton. Chaos and Time-Series Analysis (англ.). — Oxford University Press, 2003..
- Chirikov B. V. «Time-dependent quantum systems» in «Chaos and quantum mechanics» // Les Houches Lecture Series, Vol. 52, pp. 443—545, Eds. M.-J. Giannoni, A. Voros, J. Zinn-Justin, Elsevier Sci. Publ., Amsterdam (1991).