Список кристаллографических групп

Кристаллографические группы, или фёдоровские группы — набор групп симметрий, которые описывают все возможные симметрии бесконечного количества периодически расположенных точек в трёхмерном пространстве. Эта классификация симметрий была сделана независимо и почти одновременно русским математиком Фёдоровым и немецким математиком Шёнфлисом. Полученные сведения играют большую роль в кристаллографии.

Легенда к списку

Символ Германа — Могена

Символ пространственной группы содержит символ решётки Браве (заглавную букву P, A, B, C, I, R или F) и международный символ точечной группы. При этом символы осей и плоскостей симметрии в символе могут изменяться на символы винтовых осей и скользящих плоскостей в соответствии с их наличием в данном конкретном кристаллическом пространстве. Символы решётки Браве передают её тип центрировки:

P — примитивная;
I — объёмноцентрированная (дополнительный узел в центре ячейки);
F — гранецентрированная (дополнительные узлы в центрах всех граней).
С, А или В — базоцентрированная (дополнительный узел в центре грани C, A или B). Решётки типов A и B называют также бокоцентрированными;
R — дважды объёмноцентрированная (два дополнительных узла на большой диагонали ячейки).

Классы

Для обозначения кристаллографических классов (точечных групп) приняты следующие обозначения (здесь буква n заменяет натуральное число, а буква m обозначает именно саму букву m):

$n$ — ось симметрии n-го порядка.
${\bar {n}}$ — инверсионная ось симметрии n-го порядка.
$m$ — плоскость симметрии.
$nm$ или $nmm$ — ось симметрии n-го порядка и n плоскостей симметрии, проходящих вдоль неё.
${\frac {n}{m}}$ — ось симметрии порядка n и плоскость симметрии, к ней перпендикулярная.
$n2$ — ось симметрии порядка n и n осей второго порядка, к ней перпендикулярных.
$n/mmm$ — ось симметрии n-го порядка и плоскости параллельные и перпендикулярные к ней.
${\bar {n}}m2$ или ${\bar {n}}2m$ (n — чётное) — инверсионная ось симметрии n-го порядка, ${\tfrac {n}{2}}$ плоскостей симметрии, проходящих вдоль неё, и ${\tfrac {n}{2}}$ осей второго порядка, к ней перпендикулярных.
${\bar {n}}m$ (n — нечётное) — инверсионная ось симметрии n-го порядка, n плоскостей симметрии, проходящих вдоль неё, и n осей второго порядка, к ней перпендикулярных.

Символ Шёнфлиса

С_n — циклические группы — группы с единственным особым направлением, представленным поворотной осью симметрии, — обозначаются буквой С, с нижним цифровым индексом n, соответствующим порядку этой оси.

С_ni — группы с единственной инверсионной осью симметрии сопровождаются нижним индексом i.
C_nv (от нем. vertikal — вертикальный) — также имеет плоскость симметрии, расположенную вдоль единственной или главной оси симметрии, которая всегда мыслится вертикальной.
C_nh (от нем. horizontal — горизонтальный) — также имеет плоскость симметрии, перпендикулярную к главной оси симметрии.

S₂, S₄, S₆ (от нем. spiegel — зеркало) — группы с единственной зеркальной осью симметрии.

C_s — для плоскости неопределённой ориентации, то есть не фиксированной ввиду отсутствия в группе иных элементов симметрии.

D_n — является группой С_n с добавочными n осями симметрии второго порядка, перпендикулярными исходной оси.

D_nh — также имеет горизонтальную плоскость симметрии.
D_nd (от нем. diagonal — диагональный) — также имеет вертикальные диагональные плоскости симметрии, которые идут между осями симметрии второго порядка.

O, T — группы симметрии с несколькими осями высшего порядка — группы кубической сингонии. Обозначаются буквой О в случае, если они содержат полный набор осей симметрии октаэдра, или буквой Т, если они содержат полный набор осей симметрии тетраэдра.

O_h и T_h — также содержат горизонтальную плоскость симметрии
T_d — также содержат диагональную плоскость симметрии

n может равняться 1, 2, 3, 4, 6.

Список всех 230 групп

Номер	Класс	Число групп	Символ Германа-Могена	Символ Шёнфлиса	Изображение
Триклинная система
1	$1$	1	$P1$	$C_{1}$
2	${\bar {1}}$	1	$P{\bar {1}}$	$C_{i}$
Моноклинная система
3-5	$2$	3	$P2$ $P2_{1}$ $C2$	$C_{2}$	Внешне человек обладает $C_{s}$ симметрией.
6-9	$m$	4	$Pm$ $Pc$ $Cm$ $Cc$	$C_{s}$
10-15	$2/m$	6	$P2/m$ $P2_{1}/m$ $C2/m$ $P2/c$ $P2_{1}/c$ $C2/c$	$C_{2h}$
Ромбическая система
16-24	$222$	9	$P222$ $P222_{1}$ $P2_{1}2_{1}2$ $P2_{1}2_{1}2_{1}$ $C222_{1}$ $C222$ $F222$ $I222$ $I2_{1}2_{1}2_{1}$	$D_{2}$	Рельсы обладают $C_{2v}$ симметрией.
25 - 46	$mm2$	22	$Pmm2$ $Pmc2_{1}$ $Pcc2$ $Pma2$ $Pca2_{1}$ $Pnc2$ $Pmn2_{1}$ $Pba2$ $Pna2_{1}$ $Pnn2$ $Cmm2$ $Cmc2_{1}$ $Ccc2$ $Amm2$ $Aem2$ $Ama2$ $Aea2$ $Fmm2$ $Fdd2$ $Imm2$ $Iba2$ $Ima2$	$C_{2v}$
47-74	$mmm$	28	$Pmmm$ $Pnnn$ $Pccm$ $Pban$ $Pmma$ $Pnna$ $Pmna$ $Pcca$ $Pbam$ $Pccn$ $Pbcm$ $Pnnm$ $Pmmn$ $Pbcn$ $Pbca$ $Pnma$ $Cmcm$ $Cmce$ $Cmmm$ $Cccm$ $Cmme$ $Ccce$ $Fmmm$ $Fddd$ $Immm$ $Ibam$ $Ibca$ $Imma$	$D_{2h}$
Тетрагональная система
75-80	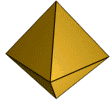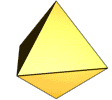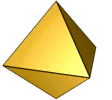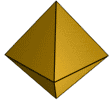$4$	6	$P4$ $P4_{1}$ $P4_{2}$ $P4_{3}$ $I4$ $I4_{1}$	$C_{4}$	$C_{4}$ Симметрия.
81-82	${\bar {4}}$	2	$P{\bar {4}}$ $I{\bar {4}}$	$S_{4}$
83-88	$4/m$	6	$P4/m$ $P4_{2}/m$ $P4/n$ $P4_{2}/n$ $I4/m$ $I4_{1}/a$	$C_{4h}$
89-98	$422$	10	$P422$ $P42_{1}2$ $P4_{1}22$ $P4_{1}2_{1}2$ $P4_{2}22$ $P4_{2}2_{1}2$ $P4_{3}22$ $P4_{3}2_{1}2$ $I422$ $I4_{1}22$	$D_{4}$
99-110	$4mm$	12	$P4mm$ $P4bm$ $P4_{2}cm$ $P4_{2}nm$ $P4cc$ $P4nc$ $P4_{2}mc$ $P4_{2}bc$ $I4mm$ $I4cm$ $I4_{1}md$ $I4_{1}cd$	$C_{4v}$
111-122	${\bar {4}}2m$	12	$P{\bar {4}}2m$ $P{\bar {4}}2c$ $P{\bar {4}}2_{1}m$ $P{\bar {4}}2_{1}c$ $P{\bar {4}}m2$ $P{\bar {4}}c2$ $P{\bar {4}}b2$ $P{\bar {4}}n2$ $I{\bar {4}}m2$ $I{\bar {4}}c2$ $I{\bar {4}}2m$ $I{\bar {4}}2d$	$D_{2d}$
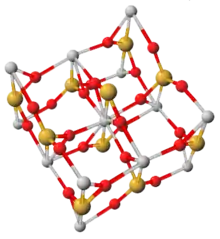123-142	$4/mmm$	20	$P4/mmm$ $P4/mcc$ $P4/nbm$ $P4/nnc$ $P4/mbm$ $P4/mnc$ $P4/nmm$ $P4/ncc$ $P4_{2}/mmc$ $P4_{2}/mcm$ $P4_{2}/nbc$ $P4_{2}/nnm$ $P4_{2}/mbc$ $P4_{2}/mnm$ $P4_{2}/nmc$ $P4_{2}/ncm$ $I4/mmm$ $I4/mcm$ $I4_{1}/amd$ $I4_{1}/acd$	$D_{4h}$	Кристаллическая решётка циркона имеет $I4_{1}/amd$ симметрию.
Тригональная система
143-146	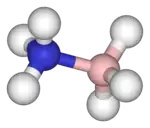$3$	4	$P3$ $P3_{1}$ $P3_{2}$ $R3$	$C_{3}$	Молекула боразана обладает $C_{3v}$ симметрией.
147-148	${\bar {3}}$	2	$P{\bar {3}}$ $R{\bar {3}}$	$C_{3i}$
149-155	$32$	7	$P312$ $P321$ $P3_{1}12$ $P3_{1}21$ $P3_{2}12$ $P3_{2}21$ $R32$	$D_{3}$
156-161	$3m$	6	$P3m1$ $P31m$ $P3c1$ $P31c$ $R3m$ $R3c$	$C_{3v}$
162-167	${\bar {3}}m$	6	$P{\bar {3}}1m$ $P{\bar {3}}1c$ $P{\bar {3}}m1$ $P{\bar {3}}c1$ $R{\bar {3}}m$ $R{\bar {3}}c$	$D_{3d}$
Гексагональная система
168-173	$6$	6	$P6$ $P6_{1}$ $P6_{5}$ $P6_{2}$ $P6_{4}$ $P6_{3}$	$C_{6}$	Пчелиные соты обладают $C_{6h}$ симметрией.
174	${\bar {6}}$	1	$P{\bar {6}}$	$C_{3h}$
175-176	$6/m$	2	$P6/m$ $P6_{3}/m$	$C_{6h}$
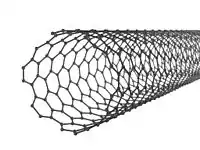177-182	$622$	6	$P622$ $P6_{1}22$ $P6_{5}22$ $P6_{2}22$ $P6_{4}22$ $P6_{3}22$	$D_{6}$	Нанотрубка может обладать $D_{6h}$ симметрией.
183-186	$6mm$	4	$P6mm$ $P6cc$ $P6_{3}cm$ $P6_{3}mc$	$C_{6v}$
187-190	${\bar {6}}m2$	4	$P{\bar {6}}m2$ $P{\bar {6}}c2$ $P{\bar {6}}2m$ $P{\bar {6}}2c$	$D_{3h}$
191-194	$6/mmm$	4	$P6/mmm$ $P6/mcc$ $P6_{3}/mcm$ $P6_{3}/mmc$	$D_{6h}$
Кубическая система
195-199	$23$	5	$P23$ $F23$ $I23$ $P2_{1}3$ $I2_{1}3$	$T$	Структура алмаза имеет $Fd{\bar {3}}m$ симметрию.
200-206	$m{\bar {3}}$	7	$Pm{\bar {3}}$ $Pn{\bar {3}}$ $Fm{\bar {3}}$ $Fd{\bar {3}}$ $Im{\bar {3}}$ $Pa{\bar {3}}$ $Ia{\bar {3}}$	$T_{h}$
207-214	$432$	8	$P432$ $P4_{2}32$ $F432$ $F4_{1}32$ $I432$ $P4_{3}32$ $P4_{1}32$ $I4_{1}32$	$O$
215-220	${\bar {4}}3m$	6	$P{\bar {4}}3m$ $F{\bar {4}}3m$ $I{\bar {4}}3m$ $P{\bar {4}}3n$ $F{\bar {4}}3c$ $I{\bar {4}}3d$	$T_{d}$
221-230	$m{\bar {3}}m$	10	$Pm{\bar {3}}m$ $Pn{\bar {3}}n$ $Pm{\bar {3}}n$ $Pn{\bar {3}}m$ $Fm{\bar {3}}m$ $Fm{\bar {3}}c$ $Fd{\bar {3}}m$ $Fd{\bar {3}}c$ $Im{\bar {3}}m$ $Ia{\bar {3}}d$	$O_{h}$

В других размерностях

У периодических структур в одномерном пространстве есть всего два типа симметрии. Они могут быть проиллюстрированы последовательностями символов:

... *- *- *- *- *- *- *- ...
... |^_^|^_^|^_^|^_^|^_^|^_^| ..

Первая бесконечная последовательность симметрична только относительно трансляции (на три символа), вторая последовательность симметрична ещё и относительно отражения.

В двумерном пространстве существует 17 типов симметрии периодических структур.

Количество групп симметрий произвольного n-мерного пространства описывается последовательностью A006227.

Последующая классификация

Группы можно разделить на симморфные и несимморфные. Симморфными называются такие симметрии, которые можно составить путём поворота вокруг осей, а также отражения от плоскостей, которые все проходят через одну точку. Симморфные пространственные группы содержат в качестве подгрупп точечные группы симметрии, отвечающие классу, к которому принадлежит данная пространственная группа.

Все 230 групп можно разделить на 32 класса. В каждом классе есть симметрия, оставляющая хотя бы одну точку пространства неподвижной. Количество элементов в классах колеблется от 1 до 28.

Классы можно разделить на системы (сингонии). Есть 7 сингоний. В каждой сингонии найдётся хотя бы одна предельная группа.

См. также

Литература

International Tables for Crystallography. Volume A: Space-group symmetry / Edited by M. I. Aroyo. — International Union of Crystallography, 2016. — ISBN 978-0-470-97423-0.

Ссылки

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.