Рассеяние света частицами
Рассеяние света частицами (англ. light scattering by particles) — процесс, при котором маленькие частицы (например, кристаллы льда, пылинки, атмосферные частицы, космическая пыль) создают оптические явления, такие как радуга, синий цвет неба, гало.
Уравнения Максвелла являются основой теоретических и вычислительных методов, описывающих рассеяние света, но поскольку точные решения уравнений Максвелла известны только для нескольких геометрических тел (таких как сферическая частица), то рассеяние света частицами является областью исследования вычислительного электромагнетизма, работающей с рассеянием и поглощением электромагнитного излучения частицами.
В случае геометрических тел, для которых известны аналитические решения (такие как сферы, скопление сфер, бесконечные цилиндры), решение обычно вычисляется в виде бесконечных рядов. В случае более сложных геометрических тел и для неоднородных частиц рассматривается и решается дискретная реализация уравнений Максвелла. Эффект многократного рассеяния света частицами изучается методами теории переноса излучения.
Относительный размер рассеивающей частицы определяется параметром размера, представляющим отношение характерного размера частицы к длине волны
Точные методы вычислений
Метод конечных разностей во временной области
Метод конечных разностей принадлежит общему классу сеточных разностных методов численного моделирования. Зависящие от времени уравнения Максвелла (в виде уравнений в частных производных) рассматриваются в дискретной форме, применяются разностные формулы для приближения частных производных. Полученные уравнения можно решать, например, методом типа leapfrog: компоненты вектора электрического поля в объеме пространства определяются для заданного момента времени, затем компоненты вектора магнитного поля в том же элементе объёма определяются для следующего момента времени; процесс повторяется.
Матрица T
Также этот метод называют методом расширенных граничных условий. Элементы матрицы получают при соотнесении граничных условий и решений уравнений Максвелла. Падающее, передаваемое и рассеиваемое поля раскладываются по сферическим векторным волновым функциям.
Приближения в вычислительных методах
Приближение Ми
Рассеяние любой сферической частицей с произвольным параметром размера рассматривается в рамках теории Ми, также называемой теорией Лоренца—Ми или теорией Лоренца—Ми—Дебая и являющейся полностью аналитическим решением уравнений Максвелла для рассеяния электромагнитного излучения сферическими частицами (Bohren and Huffman, 1998).
Для более сложных структур, таких как сферы с оболочкой, мультисферы, сфероиды, бесконечные цилиндры, существуют обобщения, выражающие решение в терминах бесконечных рядов. Существуют программы, позволяющие исследовать рассеяние света в приближении Ми для сфер, систем сферических оболочек и цилиндров.
Дискретное дипольное приближение
Существует несколько методов для вычисления рассеяния излучения на частицах произвольной формы. Дискретное дипольное приближение является приближением непрерывного тела с помощью конечного набора поляризуемых точек. Точки приобретают дипольный момент в результате отклика на локальное электрическое поле. Диполи таких точек взаимодействуют друг с другом посредством электрических полей.
Приближённые методы
Рэлеевское рассеяние
Рэлеевское рассеяние представляет собой рассеяние света или другого электромагнитного излучения частицами гораздо меньших размеров, чем длина волны света. Рэлеевское рассеяние можно определить как рассеяние при малом параметре размера .
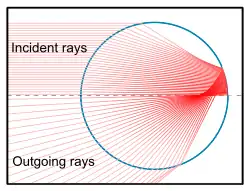
Геометрическая оптика
Метод трассировки лучей можно применять для исследования рассеяния света на сферических и несферических частицах при условии, что размер частицы гораздо больше длины волны света. Свет при этом можно считать набором отдельных лучей, но ширина лучей должна быть гораздо больше длины волны и меньше размера частицы. Лучи, ударяющиеся о поверхность частицы, отражаются, преломляются и дифрагируют. Лучи уходят от частицы под разными углами с различной амплитудой и фазой. Метод трассировки лучей используется для описания таких оптических явлений как радуга, гало на шестиугольных кристаллах льда.
Литература
- Barber,P.W. and S.C. Hill, Light scattering by particles : computational methods, Singapore ; Teaneck, N.J., World Scientific, c1990, 261 p.+ 2 computer disks (3½ in.), ISBN 9971-5-0813-3, ISBN 9971-5-0832-X (pbk.)
- Bohren, Craig F. and Donald R. Huffman, Title Absorption and scattering of light by small particles, New York : Wiley, 1998, 530 p., ISBN 0-471-29340-7, ISBN 978-0-471-29340-8
- Hulst, H. C. van de, Light scattering by small particles, New York, Dover Publications, 1981, 470 p., ISBN 0-486-64228-3.
- Kerker, Milton, The scattering of light, and other electromagnetic radiation, New York, Academic Press, 1969, 666 p.
- Mishchenko, Michael I., Joop W. Hovenier, Larry D. Travis, Light scattering by nonspherical particles: theory, measurements, and applications, San Diego : Academic Press, 2000, 690 p., ISBN 0-12-498660-9.
- Stratton, Julius Adams, Electromagnetic theory, New York, London, McGraw-Hill book company, inc., 1941. 615 p.