Последовательность Хофштадтера
Последовательность Хофштадтера — это одна из последовательностей из семейства целочисленных последовательностей, определённых нелинейными рекуррентными формулами.
Последовательности из книги Гёдель, Эшер, Бах: эта бесконечная гирлянда
Первые последовательности Хофштадтера описал Дуглас Хофштадтер в своей книге Гёдель, Эшер, Бах. Последовательности показаны в порядке их представления в главе III на фигурах и фоне (последовательность Фигура-Фигура) и в главе V на рекурсивных структурах и процессах (остальные последовательности).
Последовательности Рисунок-Рисунок Хофштадтера
Последовательности Рисунок-Рисунок Хофштадтера (R и S) — это пара комплементарных целочисленных последовательностей. Последовательность {R} определяется следующим образом[1][2]
а последовательность {S(n)} определяется как строго возрастающая последовательность положительных целых чисел, отсутствующих в {R(n)}. Первые несколько членов этих последовательностей
Последовательность G Хофштадтера
Последовательность G Хофштадтера определяется следующим образом[3][4]
Несколько первых членов этой последовательности
Последовательность H Хофштадтера
Последовательность H Хофштадтера определяется следующим образом[3][5]
Несколько первых членов этой последовательности
Женские и мужские последователи Хофштадтера
Женские (F) и мужские (M) последователи Хофштадтера определяются следующим образом[3][6]
Несколько первых членов этих последовательностей
Последовательность Q Хофштадтера
Последовательность Q Хофштадтера определяется следующим образом[3][7]:
Несколько первых членов этой последовательности
- 1, 1, 2, 3, 3, 4, 5, 5, 6, 6, 6, 8, 8, 8, 10, 9, 10, 11, 11, 12, ... (последовательность A005185 в OEIS)
Хофштадтер назвал члены последовательности «Q-числами» [3]. Таким образом 6-ое число Q равно 4. Представление последовательности Q в книге Хофштадтера, фактически, является первым упоминанием мета-последовательностей Фибоначчи в литературе[8].
В то время как числа Фибоначчи определяются суммированием двух предыдущих членов, предыдущие два члена последовательности Q определяют, насколько нужно отодвинуться назад, чтобы взять члены последовательности для суммирования. Индексы для суммирования задаются той же последовательностью Q.
Q(1), первый элемент последовательности, используется только для вычисления Q(3) [9].
Хотя последовательность Q выглядит хаотической[3][10][11][12], подобно многим другим мета-последовательностям Фибоначчи, её члены можно сгруппировать в блоки[13][14]. Для последовательности Q k-ый блок имеет 2k членов[15]. Более того, для g, принадлежащему блоку, которому принадлежит Q-число, два члена, используемые для вычисления Q-числа, называемые родителями, большей частью находятся в блоке g − 1 и только несколько членов находятся в блоке g − 2, но никогда в более ранних блоках[16].
Большинство из таких находок являются эмпирическими наблюдениями, поскольку ничего до настоящего времени не было доказано строго о последовательности Q[17][18][19]. В частности, неизвестно, является последовательность вполне определённой для всех n. То есть не «умирает» ли последовательность в некоторой точке, пытаясь использовать член последовательности слева от первого члена Q(1).[12][17][19]
Пример для понимания алгоритма:
например надо подставлять значения Q(1) = 1, Q(2)=1 (по условию).
Q(3) = Q(3-1)+Q(3-1) = Q(2)+ Q(2) = 2
Q(4) = (Q(4-Q(3))+Q(4-Q(2)) = Q(4-2)+Q(4-1) = Q(2)+Q(3) = 1+2=3
Обобщения Q последовательности
Семейство Хофштадтера–Хубера Qr,s(n)
20 лет спустя после описания Хофштадтером последовательности Q, Хофштадтер и Грег Хубер использовали символ Q для обобщения последовательности Q до семейства последовательностей, а исходную последовательность Q переименовали в последовательность U [19].
Исходная последовательность Q обобщается путём замены (n − 1) и (n − 2) на (n − r) и (n − s) соответственно[19].
Это привело к семейству последовательностей
где s ≥ 2 и r < s.
При (r,s) = (1,2) получаем оригинальную последовательность Q, так что она является членом этого семейства. В настоящее время известны только три последовательности семейства Qr,s, а именно, последовательность U с (r,s) = (1,2) (оригинальная последовательность Q)[19], последовательность V с (r,s) = (1,4)[20] и последовательность W с (r,s) = (2,4)[19]. Только для последовательности V, которая не ведёт себя столь хаотически, как две другие, доказано, что она не «умирает»[19]. Подобно исходной последовательности Q, ничего не было доказано строго для последовательности W[19].
Несколько первых членов последовательности V
- 1, 1, 1, 1, 2, 3, 4, 5, 5, 6, 6, 7, 8, 8, 9, 9, 10, 11, 11, 11, ... (последовательность A063882 в OEIS)
Несколько первых членов последовательности W
- 1, 1, 1, 1, 2, 4, 6, 7, 7, 5, 3, 8, 9, 11, 12, 9, 9, 13, 11, 9, ... (последовательность A087777 в OEIS)
Для других значений (r,s) последовательности рано или поздно «умирают», т.е. существует n, для которого значение Qr,s(n) не определено, поскольку n − Qr,s(n − r) < 1[19].
Семейство последовательностей Fi,j(n)
В 1998 Клаус Пинн, учёный из Мюнстерского университета (Германия) при тесном контакте с Хофштадтером, предложил другое обобщение последовательности Q Хофштадтера, и назвал полученные последовательности F-последовательностями[21].
Семейство последовательностей Пинна Fi,j определяется следующим образом:
Таким образом, Пинн ввёл дополнительные константы i и j, которые сдвигают индексы суммируемых членов влево (то есть ближе к началу последовательности)[21].
Только последовательности F с (i,j) = (0,0), (0,1), (1,0) и (1,1), первая из которых является исходной последовательностью Q, оказываются вполне определёнными[21]. В отличие от Q(1), первые элементы последовательностей Пинна Fi,j(n) используются для вычисления других элементов в последовательности, если одна из дополнительных констант равна 1.
Первые несколько членов последовательности F0,1 Пинна
10000-долларовая последовательность Хофштадтера — Конвея
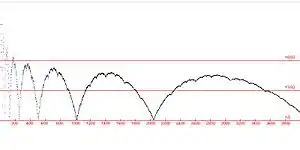
10000-долларовая последовательность Хофштадтера-Конвея определяется следующим образом[22]
Первые несколько членов последовательности
- 1, 1, 2, 2, 3, 4, 4, 4, 5, 6, 7, 7, 8, 8, 8, 8, 9, 10, 11, 12, … (последовательность A004001 в OEIS)
Последовательность получила такое название из-за того, что Джон Хортон Конвей объявил о премии в $10000 любому, кто продемонстрирует определённый результат об асимптотическом поведении последовательности. Премию, уменьшившуюся до $1000, получил Коллин Маллоуз[23]. В частной беседе с Клаусом Пинном Хофштадтер позднее утверждал, что он нашёл последовательность и её структуру где-то за 10-15 лет до объявления Конвеем премии[10].
Примечания
- Hofstadter, 1980, с. 73.
- Weisstein, Eric W. Hofstadter Figure-Figure Sequence (англ.) на сайте Wolfram MathWorld.
- Hofstadter, 1980, с. 137.
- Weisstein, Eric W. Hofstadter G-Sequence (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Hofstadter H-Sequence (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Hofstadter Male-Female Sequences (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Hofstadter's Q-Sequence (англ.) на сайте Wolfram MathWorld.
- Emerson, 2006, с. 1, 7.
- Pinn, 1999, с. 5–6.
- Pinn, 1999, с. 3.
- Pinn, 2000, с. 1.
- Emerson, 2006, с. 7.
- Pinn, 1999, с. 3–4.
- Balamohan, Kuznetsov, Tanny, 2007, с. 19.
- Pinn, 1999, с. Abstract, 8.
- Pinn, 1999, с. 4–5.
- Pinn, 1999, с. 2.
- Pinn, 2000, с. 3.
- Balamohan, Kuznetsov, Tanny, 2007, с. 2.
- Balamohan, Kuznetsov, Tanny, 2007.
- Pinn, 2000, с. 16.
- Weisstein, Eric W. Hofstadter-Conway $10,000 Sequence (англ.) на сайте Wolfram MathWorld.
- Tempel.
Литература
- Michael Tempel. Easy as 1 1 2 2 3.
- B. Balamohan, A. Kuznetsov, Stephan M. Tanny. On the Behaviour of a Variant of Hofstadter's Q-Sequence. — Journal of Integer Sequences. — Waterloo, Ontario (Canada): University of Waterloo, 2007. — Т. 10.
- Nathaniel D. Emerson. [1530-7638 A Family of Meta-Fibonacci Sequences Defined by Variable-Order Recursions]. — Journal of Integer Sequences. — Waterloo, Ontario (Canada): University of Waterloo, 2006. — Т. 9.
- Douglas Hofstadter. Gödel, Escher, Bach: an Eternal Golden Braid. — Penguin Books, 1980. — ISBN 0-14-005579-7.
- Klaus Pinn. Order and Chaos in Hofstadter's Q(n) Sequence // Complexity. — 1999. — Т. 4, вып. 3. — С. 41–46. — doi:10.1002/(SICI)1099-0526(199901/02)4:3<41::AID-CPLX8>3.0.CO;2-3. — arXiv:chao-dyn/9803012v2.
- Klaus Pinn. A Chaotic Cousin of Conway's Recursive Sequence // Experimental Mathematics. — 2000. — Т. 9, вып. 1. — С. 55–66. — arXiv:cond-mat/9808031.