Полиэдр
Полиэдром называется объединение многогранников не обязательно одинаковой размерности. В геометрии многогранник (множественное число многогранников) — это трехмерная фигура с плоскими многоугольными гранями, прямыми ребрами и острыми углами или вершинами. Слово многогранник происходит от классического греческого πολεεδρον, как poly- (стебель πολύς, "много") + -hedron (формаδδρα, "основание" или "сиденье"). Выпуклый многогранник — это выпуклая оболочка конечного числа точек, а не всех на одной плоскости. Кубики и пирамиды являются примерами выпуклых многогранников.
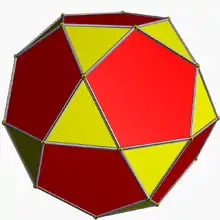



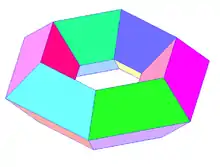
Многогранник — это трехмерный пример более общего многогранника в любом числе измерений.
Разбиение полиэдра на симплексы называется симплициальным комплексом.
Понятие полиэдра используется в теории симплициальных гомологий.
Иногда полиэдром называют обычный многогранник размерности 3.
Определение
Выпуклые многогранники хорошо определены, с несколькими эквивалентными стандартными определениями. Однако формальное математическое определение многогранников, которые не обязательно должны быть выпуклыми, было проблематичным. Многие определения "многогранника" были даны в определенных контекстах, некоторые из них более строгие, чем другие, и нет универсального согласия относительно того, какое из них выбрать. Некоторые из этих определений исключают формы, которые часто считались многогранниками (например, самопересекающиеся многогранники), или включают формы, которые часто не считаются допустимыми многогранниками (например, твердые тела, границы которых не являются многообразиями). Как заметил Бранко Грюнбаум: "первородный грех в теории многогранников восходит к Евклиду, а также через Кеплера, Пуансо, Коши и многих других. На каждом этапе авторы не смогли определить, что такое многогранники".[1]
Тем не менее, существует общее мнение, что многогранник-это твердое тело или поверхность, которая может быть описана его вершинами (угловыми точками), ребрами (отрезками линий, соединяющими определенные пары вершин), гранями (двумерными многоугольниками), а иногда и его трехмерным внутренним объемом. Можно различать эти различные определения в зависимости от того, описывают ли они многогранник как твердое тело, описывают ли они его как поверхность или описывают его более абстрактно, основываясь на его геометрии падения.
Общее и несколько наивное определение многогранника состоит в том, что это твердое тело, граница которого может быть покрыта конечным числом плоскостей, или что это твердое тело, образованное как объединение конечного числа выпуклых многогранников.[2] Естественные уточнения этого определения требуют, чтобы твердое тело было ограничено, имело связную внутреннюю часть и, возможно, также имело связную границу. Грани такого многогранника можно определить как связанные компоненты частей границы внутри каждой из плоскостей, покрывающих ее, а ребра и вершины-как отрезки линий и точки, в которых эти грани встречаются. Однако многогранники, определенные таким образом, не включают в себя самопересекающиеся Звездные многогранники, их грани не могут образовывать простые многоугольники, а некоторые ребра могут принадлежать более чем двум граням. Определения, основанные на идее ограничивающей поверхности, а не твердого тела, также распространены. Например, О'Рурк (1993) определяет многогранник как объединение выпуклых многоугольников (его граней), расположенных в пространстве так, что пересечение любых двух многоугольников является общей вершиной или ребром или пустым множеством и так, что их объединение является многообразием. Если плоская часть такой поверхности сама по себе не является выпуклым многоугольником, О'Рурк требует, чтобы она была разделена на меньшие выпуклые многоугольники с плоскими двугранными углами между ними. Несколько более обобщенно Грюнбаум определяет акоптический многогранник как совокупность простых многоугольников, образующих вложенное многообразие, причем каждая вершина инцидентна по крайней мере трем ребрам, а каждая из двух граней пересекается только в общих вершинах и ребрах каждого из них.[3] Многогранники Кромвеля дают аналогичное определение, но без ограничения трех ребер на вершину. Опять же, этот тип определения не охватывает самопересекающиеся многогранники. Подобные понятия лежат в основе топологических определений многогранников, как подразделений топологического многообразия на топологические диски (грани), попарные пересечения которых должны быть точками (вершинами), топологическими дугами (ребрами) или пустым множеством. Однако существуют топологические многогранники (даже со всеми гранями треугольников), которые не могут быть реализованы как акоптические многогранники.
Один из современных подходов основан на теории абстрактных многогранников. Они могут быть определены как частично упорядоченные множества, элементами которых являются вершины, ребра и грани многогранника. Элемент вершины или ребра меньше элемента ребра или грани (в этом частичном порядке), когда вершина или ребро являются частью ребра или грани. Кроме того, можно включить специальный нижний элемент этого частичного порядка (представляющий пустое множество) и верхний элемент, представляющий весь многогранник. Если сечения частичного порядка между элементами, расположенными на расстоянии трех уровней друг от друга (то есть между каждой гранью и нижним элементом, а также между верхним элементом и каждой вершиной), имеют ту же структуру, что и абстрактное представление многоугольника, то эти частично упорядоченные множества несут точно такую же информацию, что и топологический многогранник. Однако эти требования часто смягчаются, вместо этого требуется только, чтобы секции между элементами, расположенными на двух уровнях друг от друга, имели ту же структуру, что и абстрактное представление отрезка линии. Это означает, что каждое ребро содержит две вершины и принадлежит двум граням, и что каждая вершина на грани принадлежит двум ребрам этой грани. Геометрические многогранники, определенные другими способами, могут быть описаны абстрактно таким образом, но также можно использовать абстрактные многогранники в качестве основы определения геометрических многогранников. Реализация абстрактного многогранника обычно рассматривается как отображение вершин абстрактного многогранника в геометрические точки, так что точки каждой грани являются копланарными.
Примечания
- Branko Grünbaum. Polyhedra with Hollow Faces (англ.) // Polytopes: Abstract, Convex and Computational / T. Bisztriczky, P. McMullen, R. Schneider, A. Ivić Weiss. — Dordrecht: Springer Netherlands, 1994. — P. 43–70. — ISBN 978-94-011-0924-6. — doi:10.1007/978-94-011-0924-6_3.
- Polyhedron, abstract - Encyclopedia of Mathematics. encyclopediaofmath.org. Дата обращения: 12 июля 2020.
- Grünbaum, Branko (1999), "Acoptic polyhedra".
Литература
- Понтрягин Л. С. Основы комбинаторной топологии. — М.: Наука, 1986
- Математическая энциклопедия. В пяти томах. Том 3, стр.151. Том 4, стр.1168. (М.: Советская энциклопедия, 1985.)