Поверхность потенциальной энергии

Поверхность потенциальной энергии применяется для описания энергии системы, в особенности множества атомов, в терминах определённых параметров, обычно — координат атомов. Поверхность может определять энергию как функцию одной или нескольких координат. Если координата только одна, то поверхность называется кривой потенциальной энергии или профилем энергии.

В некоторых случаях полезно использовать аналогию с ландшафтом: если у системы две степени свободы, то значение энергии можно представить как высоту в зависимости от двух координат.[1]

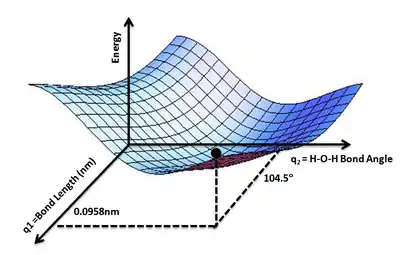
Поверхность потенциальной энергии для молекулы воды: минимум энергии соответствует оптимальной структуре молекулы — длина химической связи составляет O-H равна 0,0958 нм, а угол H-O-H равен 104,5°

Понятие поверхности потенциальной энергии применяется в физике и химии, особенно в теоретических разделах этих дисциплин, и может использоваться для теоретического исследования свойств структур атомов, например, для определения формы с минимальной энергией для молекулы или для вычисления скорости химических реакций.

Математическое определение и вычисления

Геометрия набора атомов может быть описана вектором r, элементы которого показывают расположение атомов. Вектор r может быть множеством декартовых координат атомов или же набором межатомных расстояний и углов.

При известном r энергия является функцией E(r) для всех рассматриваемых значений r. Пользуясь аналогией с ландшафтом, можно рассматривать величину E как высоту "ландшафта энергии", то есть как меру высоты поверхности потенциальной энергии.

Для изучения химических реакций с помощью поверхности потенциальной энергии как функции положения атомов необходимо вычислять энергию для каждого рассматриваемого взаимного расположения частиц. Методы расчёта энергии для конкретного относительного расположения частиц описаны в статьях по вычислительной химии, особое внимание уделяется нахождению приближённого значения энергии E(r) для получения информации о энергии и положении частиц с высоким разрешением.

Для очень простых химических систем или при введении упрощающих предположений о взаимодействии атомов иногда возможно использовать аналитические выражения для энергии в виде функции расположения атомов. Примером является потенциал Лондона-Эйринга-Полани-Сато[2][3][4] для системы H + H2 в виде функции трёх расстояний H-H.

Для более сложных систем вычисление энергии определённого расположения атомов зачастую представляет собой слишком сложную вычислительную задачу, поэтому получить точки поверхности с высоким разрешением сложно. Для таких систем возможным подходом является вычисление только уменьшенного количества точек на поверхности и затем применение метода интерполяции, например интерполяции Шепарда.[5]

Применение

Поверхность потенциальной энергии является удобным инструментом для исследования молекулярной геометрии и динамики химических реакций. На поверхности вычисляются только необходимые точки. В целом точки классифицируют по значениям первой и второй производной энергии по координатам, то есть по величине градиента и кривизны. Стационарные точки (с нулевым градиентом) имеют физический смысл: минимум энергии соответствует физически устойчивым образцам, а седловые точки соответствуют переходным состояниям, точка с наибольшей высотой является координатой реакции.

Поверхности притяжения и отталкивания

Поверхности потенциальной энергии для химических реакций можно классифицировать как поверхности притяжения и отталкивания по сравнению величины длины химических связей.[6][7] Для реакции типа A + B—C → A—B + C, увеличение длины химической связи A—B определяется как R*AB = RAB − R0AB, где RAB является длиной химической связи A—B в переходном состоянии, а R0AB в молекуле продукта реакции. Аналогично для связи, разрушающейся при реакции, R*BC = RBC − R0BC, где R0BC относится к молекуле реагента.[8]

Для экзотермических реакций поверхность потенциальной энергии при R*AB > R*BC такова, что переходное состояние достигается при приближении реактантов друг к другу. После переходного состояния длина химической связи A—B продолжает уменьшаться, при этом большая часть выделяющейся энергии преобразуется в энергию колебаний.[8][9] Примером является гарпунный механизм K + Br2 → K—Br + Br.[8] Молекулы продукта реакции, переведённые под воздействием колебаний в возбуждённое состояние, могут быть обнаружены по инфракрасной хемолюминесценции.[10][11]

Поверхность потенциальной энергии для реакции H + Cl2 → HCl + Cl такова, что R*HCl < R*ClCl и состояние перехода достигается, когда продукты реакции разделяются.[8][9] Для реакции, в которой атом A (в данном случае H) легче, чем B и C, энергия реакции выделяется в основном в виде кинетической энергии продуктов реакции.[8] Для реакции типа F + H2 → HF + H, где атом A тяжелее чем B и C, происходит смешанное выделение энергии, как колебательной, так и энергии перемещения.[8]

В эндотермических реакциях тип поверхности определяет тип энергии, который наиболее эффективен в ходе реакции.[12]

История

Понятие поверхности потенциальной энергии для химических реакций впервые было предложено французским физиком Рене Марселеном в 1913 году.[13] Первое полуэмпирическое вычисление поверхности потенциальной энергии было представлено для реакции H + H2 Генри Эйрингом и Майклом Полани в 1931 году. Эйринг использовал поверхности потенциальной энергии для вычисления постоянных скорости реакции в теории переходных состояний в 1935 году.

Примечания
  1. Potential-energy (reaction) surface in Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997)
  2. Sato, S. A New Method of Drawing the Potential Energy Surface (англ.) // Bulletin of the Chemical Society of Japan : journal. — 1955. — Vol. 28, no. 7. — P. 450. — doi:10.1246/bcsj.28.450.On a New Method of Drawing the Potential Energy Surface (англ.) // Journal of Chemical Physics : journal. — 1955. — Vol. 23, no. 3. — P. 592. — doi:10.1063/1.1742043. — .
  3. Keith J. Laidler, Chemical Kinetics (3rd ed., Harper & Row 1987) p.68-70 ISBN 0-06-043862-2
  4. Steinfeld J.I., Francisco J.S. and Hase W.L. Chemical Kinetics and Dynamics (2nd ed., Prentice-Hall 1998) p.201-2 ISBN 0-13-737123-3
  5. Moving least-squares enhanced Shepard interpolation for the fast marching and string methods, Burger SK1, Liu Y, Sarkar U, Ayers PW, J Chem Phys. 2009 130(2) 024103. doi: 10.1063/1.2996579.
  6. Attractive potential-energy surface in Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997)
  7. Repulsive potential-energy surface in Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford (1997)
  8. Keith J. Laidler, Chemical Kinetics (3rd ed., Harper & Row 1987) p.461-8 ISBN 0-06-043862-2
  9. Steinfeld J.I., Francisco J.S. and Hase W.L. Chemical Kinetics and Dynamics (2nd ed., Prentice-Hall 1998) p.272-4 ISBN 0-13-737123-3
  10. Steinfeld J.I., Francisco J.S. and Hase W.L. Chemical Kinetics and Dynamics (2nd ed., Prentice-Hall 1998) p.263 ISBN 0-13-737123-3
  11. Atkins P. and de Paula J. Physical Chemistry (8th ed., W.H.Freeman 2006) p.886 ISBN 0-7167-8759-8
  12. Atkins P. and de Paula J. Physical Chemistry (8th ed., W.H.Freeman 2006) p.889-890 ISBN 0-7167-8759-8
  13. Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics Errol G. Lewars, 2nd ed. (Springer 2011) p.21 ISBN 978-9048138616
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.