Паутинообразная модель

Регулярно повторяющиеся циклы производства и цены по сырьевым товарам были отмечены ещё в работах С. Беннер «Пророчество Беннера будущих взлетов и падения цен»[1] 1876 года, Эзекиель М. и Хаас Г. С. «Факторы, влияющие на цены свинины»[2] 1926 года и статьи Артура Ханау «Прогноз цен на свинину»[3] 1927 года, которые сформировали свиной бизнес - цикл, на основе которого в свою очередь были открыты циклы Китчина[4].

Постоянные колебания цен на рынках продукции, чьё производство занимает значительное время, а хранение с небольшим сроком, где произведенное количество зависит от цены, ожидаемое на момент продажи, как и предложение на момент продажи определяет текущую цену, были параллельно и независимо друг от друга впервые исследованы в 1930 году в статьях голландского экономиста Яна Тинбергена «Определение и интерпретация кривых предложения: описание»[5], американского экономиста Генри Шульца «Значения статического спроса»[6] и итальянского экономиста Умберто Ричи «Синтетическая экономика»[7]. В 1934 году вышла статья американского экономиста Н. Калдора «Определение статистического равновесия»[8], в которой модель получила название паутинообразной на основании того, что график кривых, отражающих изменения цен, образовывают паутину[9].

Модель имеет ряд предпосылок[10]:

• совершенная конкуренция.

Цены устанавливаются на основе колебаний спроса и предложения, а вне состояния равновесия не обязательно возвращаются к нему[11].

Сходящаяся спираль

Раскручивающаяся спираль

Постоянные колебания

Нелинейные колебания

Производитель на основе текущей цены ${\displaystyle P}$ определяет количество ${\displaystyle Q}$ продукции, которое поставит на рынок в предстоящий период. Если текущая цена ${\displaystyle P}$ высока, то производители начинают увеличивать свой объём производства, чтобы в конце своего производственного цикла сделать поставку своей продукции на рынок. Производители в рамках собственной кривой предложения действуют с запозданием, так как связывают своё количество последующего периода на основе текущей цены, причем период — это производственный цикл партии[10].

Равновесие модели фиксируется в точке пересечения кривой предложения ${\displaystyle SS}$ и кривой спроса ${\displaystyle DD}$ в точке ${\displaystyle E}$, где количество ${\displaystyle Q^{*}}$, которое потребуется покупателям, совпадает с количеством, которое производители готовы поставить[10].

Сходящаяся спираль

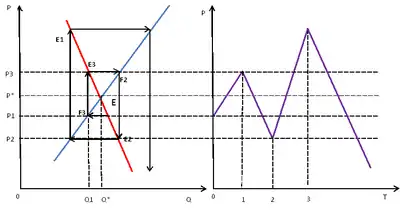
Если крутизна линии предложения больше, чем крутизна падающей линии спроса, то колебания постепенно затухают, спираль закручивается внутрь, достигается равновесие до следующего экзогенного толчка:

${\displaystyle {\frac {dQ^{S}/Q}{dP^{S}/P}}<\left|{\frac {dQ^{D}/Q}{dP^{D}/P}}\right|,}$

В случае изменения (падения) количества производства до уровня ${\displaystyle Q_{1}}$, что соответствует точки ${\displaystyle E}$ на кривой спроса, равной цене ${\displaystyle P_{1}}$, что выше равновесной цены ${\displaystyle P^{*}}$. Новая цена стимулирует производителей производить больше, равной точки ${\displaystyle F2}$ на линии предложения, но покупатели готовы покупать только по цене ${\displaystyle P^{2}}$ , что соответствует точке ${\displaystyle E2}$ на кривой спросе, а значит производители принимают решение сократить производство до уровня ${\displaystyle F3}$ на кривой предложения, что позволяет поднять цены до уровня ${\displaystyle P^{3}}$, что соответствует точке ${\displaystyle E3}$ на кривой спроса и так далее до точки равновесия ${\displaystyle E}$[10].

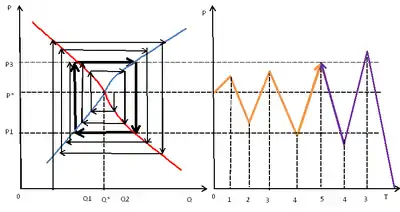
Раскручивающаяся спираль

Если линяя предложения обладает меньшей крутизной, чем линяя спроса, то спираль раскручивается, колебания увеличиваются[11]:

${\displaystyle {\frac {dQ^{S}/Q}{dP^{S}/P}}>\left|{\frac {dQ^{D}/Q}{dP^{D}/P}}\right|.}$

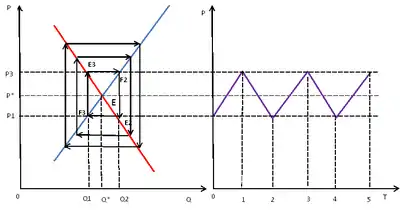
Постоянные колебания

Если линяя спроса и предложения обладают одинаковой крутизной, то равномерные колебания являются постоянными, бесконечно колеблясь вокруг положения равновесия[11]:

${\displaystyle {\frac {dQ^{S}/Q}{dP^{S}/P}}=\left|{\frac {dQ^{D}/Q}{dP^{D}/P}}\right|.}$

Нелинейные колебания

Кривые спроса и предложения могут иметь такие формы, при которых крутизна кривой предложения в точке равновесия меньше, чем кривой спроса. При незначительных изменениях колебания раскручиваются, а при значительных изменениях колебания имеют затухающие колебания до определенного уровня, где имеют постоянные колебания[10].

Положительное применение модели отмечается при анализе рынка кукурузы и свинины в начале XX века, денежной теории и теории экономических циклов в 1950-х годах, на рынке труда юристов, врачей и инженеров в 1970-х годах[12], российского фармацевтического рынка[13].

Ряд исследователей отмечают слабые места модели[12]:

• продолжение выпуска продукции в условиях ожидания производителями своих потерь;
• отсутствие чётких определений и перехода от краткосрочной к долгосрочной кривой предложения;
• механизм ожиданий, при которых производители могут повысить точность своих оценок, обнаружив схему ошибок прогноза сами и включив их в свои прогнозы;
• причина использования механизма прогнозирования производителями;
• отсутствие корреляции ошибок в прогнозе, при которых пример прошлых прогнозных ошибок нельзя использовать для повышения точности прогнозов;
• модель предсказывает более короткий ценовой цикл, чем тот, который наблюдается.

• Модель нащупывания.