Параметры Стокса

Сфера Пуанкаре позволяет визуализировать параметры Стокса как проекции вектора ${\displaystyle I}$ на координатные оси

Изображение поляризаций на сфере Пуанкаре

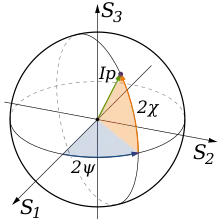
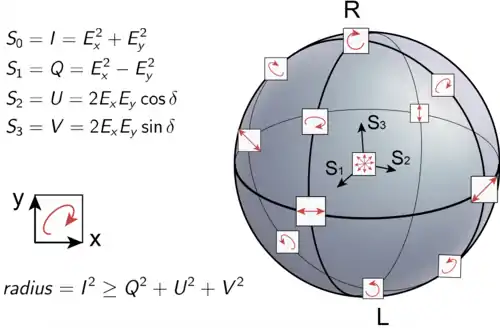
В случае плоской монохроматической волны параметры Стокса связаны с параметрами поляризационного эллипса следующим образом[2]:

${\displaystyle {\begin{aligned}S_{0}&=I=E_{a}^{2}+E_{b}^{2}\\S_{1}&=Q=I\cos 2\psi \cos 2\chi \\S_{2}&=U=I\sin 2\psi \cos 2\chi \\S_{3}&=V=I\sin 2\chi \end{aligned}}}$

Поляризационный эллипс

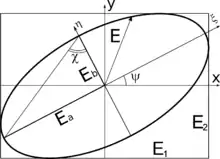
Здесь ${\displaystyle E_{a}}$ и ${\displaystyle E_{b}}$ — большая и малая полуоси поляризационного эллипса, ${\displaystyle \psi }$— угол поворота поляризационного эллипса относительно произвольной лабораторной системы координат — носит название азимута эллиптически-поляризованного излучения[3] (или кратко — азимут), а угол ${\displaystyle \chi }$, определяемый из условия отношения малой полуоси к большой ${\displaystyle \mathrm {tg} \,{\chi }=E_{b}/E_{a}}$— угол эллиптичности эллипса поляризации. Нетрудно заметить, что ${\displaystyle S_{1}}$, ${\displaystyle S_{2}}$ и ${\displaystyle S_{3}}$ являются проекциями ${\displaystyle S_{0}}$ на некие координатные оси. В итоге независимыми являются всего три параметра Стокса, поскольку:

${\displaystyle I^{2}=Q^{2}+U^{2}+V^{2}}$

Параметры Стокса можно связать с величинами, непосредственно измеряемыми. Пусть ${\displaystyle E_{1}}$ и ${\displaystyle E_{2}}$ — амплитуды изменения вектора ${\displaystyle {\vec {E}}}$ в двух произвольных ортогональных направлениях, а ${\displaystyle \delta }$ — разность фаз колебаний в этих направлениях. Тогда:

${\displaystyle {\begin{aligned}S_{0}&=I=E_{1}^{2}+E_{2}^{2}\\S_{1}&=Q=E_{1}^{2}-E_{2}^{2}\\S_{2}&=U=2E_{1}E_{2}\cos \delta \\S_{3}&=V=2E_{1}E_{2}\sin \delta \end{aligned}}}$

Примечание: наряду с вариантами обозначений ${\displaystyle S_{0}}$, ${\displaystyle S_{1}}$, ${\displaystyle S_{2}}$, ${\displaystyle S_{3}}$ или ${\displaystyle I}$, ${\displaystyle Q}$, ${\displaystyle U}$, ${\displaystyle V}$ в некоторых научных традициях можно встретить обозначения параметров вектора ${\displaystyle I}$, ${\displaystyle M}$, ${\displaystyle C}$, ${\displaystyle S}$ или ${\displaystyle I}$, ${\displaystyle P_{1}}$, ${\displaystyle P_{2}}$, ${\displaystyle P_{3}}$ или ${\displaystyle S_{1}}$, ${\displaystyle S_{2}}$, ${\displaystyle S_{3}}$, ${\displaystyle S_{4}}$.

Частные случаи

Выразим с помощью параметров Стокса линейную поляризацию. В этом случае разность фаз в любых ортогональных направлениях должна составлять ${\displaystyle \delta =m\pi }$, где ${\displaystyle m}$ — целое число. Тогда получаем

${\displaystyle {\begin{aligned}I&=E_{1}^{2}+E_{2}^{2}=E_{a}^{2}+E_{b}^{2}\\Q&=I\cos {2\chi }\cos {2\psi }=I{\frac {1}{I}}{\sqrt {I^{2}-(2E_{1}E_{2})^{2}\sin ^{2}\delta }}\cos {2\psi }=I\cos {2\psi }\\U&=I\cos {2\chi }\sin {2\psi }=I{\frac {1}{I}}{\sqrt {I^{2}-(2E_{1}E_{2})^{2}\sin ^{2}\delta }}\sin {2\psi }=I\sin {2\psi }\\V&=I\sin {2\chi }=I{\frac {2E_{1}E_{2}}{I}}\sin {\delta }=0\end{aligned}}}$

Предположим, что лабораторная ось отсчёта была выбрана горизонтально, как часто это и делается. Если ${\displaystyle \psi =0}$, то мы получим горизонтальную линейную поляризацию, если ${\displaystyle \psi =\pm {\frac {\pi }{2}}}$, то это будет вертикальная линейная поляризация.

В таблице приведены значения параметров Стокса для трех частных случаев

Поляризация	Параметры Стокса
	${\displaystyle I}$	${\displaystyle Q}$	${\displaystyle U}$	${\displaystyle V}$
Линейная	${\displaystyle I}$	${\displaystyle I\cos {2\psi }}$	${\displaystyle I\sin {2\psi }}$	${\displaystyle 0}$
Правая круговая	${\displaystyle I}$	${\displaystyle 0}$	${\displaystyle 0}$	${\displaystyle I}$
Левая круговая	${\displaystyle I}$	${\displaystyle 0}$	${\displaystyle 0}$	${\displaystyle -I}$

Примеры

Ниже приведены векторы Стокса для некоторых простых вариантов поляризации света.

Горизонтальная поляризация	Вертикальная поляризация	Линейная поляризация (+45°)	Линейная поляризация (−45°)
${\displaystyle {\begin{pmatrix}1\\1\\0\\0\end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}1\\0\\1\\0\end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}1\\0\\-1\\0\end{pmatrix}}}$
Левая круговая поляризация	Правая круговая поляризация
${\displaystyle {\begin{pmatrix}1\\0\\0\\-1\end{pmatrix}}}$	${\displaystyle {\begin{pmatrix}1\\0\\0\\1\end{pmatrix}}}$
Неполяризованный свет
${\displaystyle {\begin{pmatrix}1\\0\\0\\0\end{pmatrix}}}$

Введем комплексную интенсивность линейно поляризованной волны

${\displaystyle {\begin{matrix}L&\equiv &|L|e^{i2\theta }\\&\equiv &Q+iU.\\\end{matrix}}}$

Можно показать, что при повороте ${\displaystyle \theta \rightarrow \theta +\theta '}$ поляризационного эллипса величины ${\displaystyle I}$ и ${\displaystyle V}$ остаются неизменными, а величины ${\displaystyle L}$, ${\displaystyle Q}$ и ${\displaystyle U}$ меняются следующим образом:

${\displaystyle {\begin{matrix}L&\rightarrow &e^{i2\theta '}L,\\Q&\rightarrow &{\mbox{Re}}\left(e^{i2\theta '}L\right),\\U&\rightarrow &{\mbox{Im}}\left(e^{i2\theta '}L\right).\\\end{matrix}}}$

Благодаря этим свойствам параметры Стокса можно свести к трем обобщенным интенсивностям:

${\displaystyle {\begin{matrix}I&\geq &0,\\V&\in &\mathbb {R} ,\\L&\in &\mathbb {C} ,\\\end{matrix}}}$

где ${\displaystyle I}$ — полная интенсивность, ${\displaystyle |V|}$ — интенсивность компоненты с круговой поляризацией, а ${\displaystyle |L|}$ — интенсивность линейно поляризованной компоненты излучения. Полная интенсивность поляризованного излучения будет ${\displaystyle I_{p}={\sqrt {|L|^{2}+|V|^{2}}}}$, а ориентация и направление вращения определяются отношениями

${\displaystyle {\begin{matrix}\theta &=&{\frac {1}{2}}\arg(L),\\h&=&\operatorname {sgn}(V).\\\end{matrix}}}$

Так как ${\displaystyle Q={\mbox{Re}}(L)}$, а ${\displaystyle U={\mbox{Im}}(L)}$, то

${\displaystyle {\begin{matrix}|L|&=&{\sqrt {Q^{2}+U^{2}}},\\\theta &=&{\frac {1}{2}}\tan ^{-1}(U/Q).\\\end{matrix}}}$

• Поляризация волн

• E. Collett, Field Guide to Polarization, SPIE Field Guides vol. FG05, SPIE (2005). ISBN 0-8194-5868-6.
• E. Hecht, Optics, 2nd ed., Addison-Wesley (1987). ISBN 0-201-11609-X.
• William H. McMaster. Polarization and the Stokes Parameters (англ.) // Am. J. Phys. : journal. — 1954. — Vol. 22. — P. 351. — doi:10.1119/1.1933744.
• William H. McMaster. Matrix representation of polarization (англ.) // Rev. Mod. Phys. : journal. — 1961. — Vol. 8. — P. 33. — doi:10.1103/RevModPhys.33.8.

• Stokes parameters and polarisation