Отсечение отрезков
Отсечение отрезков — это процесс в компьютерной графике удаления прямых или частей прямых вне зоны внимания. Обычно любая прямая или часть прямой, не принадлежащая видимой области, удаляется.
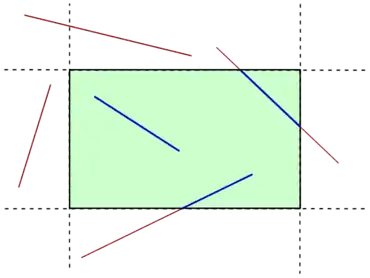
Существуют два общих алгоритма отсечения отрезков — алгоритм Коэна — Сазерленда и алгоритм Ляна – Барски.
Метод отсечения отрезков состоит из различных частей. Сначала осуществляются проверки на данном отрезке с целью определения, не лежит ли он вне видимой области. После этого вычисляются пересечения с одной или более границ[1].
Определение, какая часть прямой находится внутри или вне рассматриваемой области, осуществляется путём рассмотрения точек прямой по отношению к пересечениям.
Алгоритм Коэна — Сазерленда
Алгоритм Коэна — Сазерленда (назван именами Дэнни Коэна и Ивана Сазерленда) — это алгоритм отсечения прямой. Алгоритм делит двумерное пространство на 9 областей, из которых только средняя часть видима.
В 1967 году работа по моделированию полёта Дэнни Коэна привела к развитию алгоритмов отсечения отрезков для двухмерной и трёхмерной компьютерной графики, созданных совместно с Иваном Сазерлендом.
Алгоритм Ляна – Барски
Алгоритм Ляна – Барски использует параметрическое уравнение прямой и неравенства, описывающие области отсекающего блока для определения пересечения прямой и отсекающего блока. С этими пересечениями становится ясно, какую часть прямой следует отрисовывать. Алгоритм существенно эффективнее алгоритма Коэна — Сазерленда, но алгоритм Коэна — Сазерленда делает тривиальные принятия или отвержения быстрее, так что его имеет смысл использовать, если бо́льшая часть прямых и отрезков следует полностью удалить из окна отсечения.
Алгоритм Кируса — Бека
Очень похож на алгоритм отсечения отрезков Ляна – Барски, который является упрощённым вариантом данного алгоритма, оптимизированного для прямоугольного окна отсечения.
Алгоритм Кируса — Бека в основном предназначен для отсечения прямой в параметрическом виде относительно выпуклого многоугольника в двумерном пространстве или выпуклого многогранника в трёхмерном пространстве[2].
Алгоритм Николл — Ли — Николла
Алгоритм Алгоритм Николл — Ли — Николла (Тина М. Николл, Робин А. Николл) является алгоритмом быстрого отсечения отрезков, который сокращает шанс отсечения отрезка несколько раз, что может происходить в алгоритме Коэна — Сазерленда. Отсекающее окно делится на несколько различных областей, зависящих от позиции начальной точки прямой, требующей отсечения.
Алгоритм быстрого отсечения
Этот алгоритм похож на алгоритм Коэна — Сазерленда. Начальная и конечная позиции классифицируются по тому, в какой порции из 9 областей они находятся. Большой оператор-переключатель переключает в специальный обработчик для каждого отдельного случая. В отличие от этого алгоритма, алгоритм Коэна — Сазерленда может отрабатывать несколько раз один и тот же случай[3].
Алгоритм O(lg N)
Алгоритм классифицирует вершины по прямой, заданной в явном виде p: ax + by + c = 0. Так как многоугольник предполагается выпуклым, а вершины упорядочены по часовой стрелке или против часовой стрелки, можно применить двоичный поиск, приводящий к сложности O(lg N)[4].
Алгоритм Скалы
Алгоритм Ска́лы основан на однородных координатах и двойственности[5]. Алгоритм может быть использован для отсечения прямой или отрезков для прямоугольного окна, а также для выпуклого многоугольника. Алгоритм основывается на классификации вершин отсекающего окна относительно полуплоскости, задаваемой прямой . Результат классификации определяет рёбра, пересекаемые прямой p. Алгоритм прост, легко реализуется и расширяется на выпуклые окна. Прямую или отрезок p можно вычислить из точек r1, r2, заданных в однородных координатах непосредственно, используя векторное произведение
или
- .
См. также
Примечания
- Renka, R. J. Line Clipping. Department of Computer Science & Engineering, University of North Texas (19 октября 2014). Дата обращения: 12 января 2016.
- Cyrus, Beck, 1978, с. 23–28.
- Sobkow, Pospisil, Yang, 1987, с. 459–467.
- Skala, 1994.
- Skala, 2005, с. 905–914.
Литература
- Cyrus M., Beck J. Generalized Two and Three Dimensional Clipping // Computers & Graphics. — 1978. — Т. 3, № 1.
- Mark S. Sobkow, Paul Pospisil, Yee-Hong Yang. A Fast Two-Dimensional Line Clipping Algorithm via Line Encoding // Computer & Graphics. — 1987. — Т. 11, № 4.
- Václav Skala. O(lg N) Line Clipping Algorithm in E2 // Computers & Graphics. — Pergamon Press, 1994. — Т. 18, № 4.
- Václav Skala. A new approach to line and line segment clipping in homogeneous coordinates // The Visual Computer. — Springer Verlag, 2005. — Т. 21, № 11. — ISSN 0178-2789.