Окружность Ламуна
В планиметрии окружность Ламуна — это специальная окружность, которую можно построить в любом треугольнике . Она содержит центры описанных окружностей шести треугольников, на которые треугольник разрезают три его медианы.[1][2] Пусть для определенности , , — 3 вершины треугольника , и пусть — его центроид (пересечение трёх медиан). Пусть , и — середины сторон , и соответственно. Тогда центры шести описанных окружностей шести треугольников, на которые треугольник разбивается медианами: , , , , и , лежат на общей окружности, которая называется окружностью Ламуна (англ. the van Lamoen circle).[2]
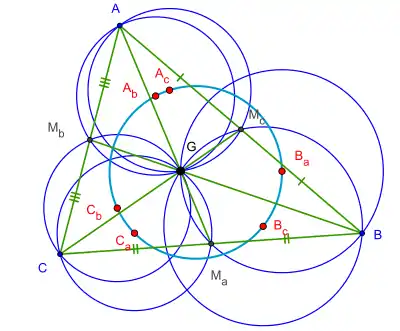
История
Окружность Ламуна так названа в честь математика Ламуна (Floor van Lamoen), который сформулировал это как задачу (проблему) в 2000 г.[3]. Доказательство было предоставлено Кин Я. Ли (Kin Y. Li) в 2001 г. [4],[5]
Свойства
Центром окружности Ламуна является точка в Энциклопедии центров треугольника К. Кимберлинга. В 2003 году Алексей Мякишев и Петер Й. Ву (Peter Y. Woo) доказали, что обратное утверждение теоремы почти всегда справедливо в следующем смысле: пусть — любая точка внутри треугольника, и , и — три его чевианы, то есть отрезки, которые соединяют каждую вершину с , продолженные до их пересечения с противоположной стороной. Тогда описанные окружности шести треугольников , , , , и лежат на одной окружности тогда и только тогда, когда является центроидом треугольника или его ортоцентром (точкой пересечения трёх его высот). [6] Более простое доказательство этого результата было дано Нгуен Минь Ха (Nguyen Minh Ha) в 2005 году.[7]
См. также
- Окружность Парри
- Окружность Лестера
Примечание
- Clark Kimberling (), X(1153) = Center of the van Lemoen circle, in the Encyclopedia of Triangle Centers Accessed on 2014-10-10.
- Eric W. Weisstein, van Lamoen circle at Mathworld. Accessed on 2014-10-10.
- Kin Y. Li (2001), Concyclic problems. Mathematical Excalibur, volume 6, issue 1, pages 1-2.
- Clark Kimberling (), X(1153) = Center of the van Lemoen circle, in the Encyclopedia of Triangle Centers Accessed on 2014-10-10
- (2002), Solution to Problem 10830. American Mathematical Monthly, volume 109, pages 396—397
- Alexey Myakishev and Peter Y. Woo (2003), On the Circumcenters of Cevasix Configuration. Forum Geometricorum, volume 3, pages 57-63.
- N. M. Ha (2005), Another Proof of van Lamoen’s Theorem and Its Converse. Forum Geometricorum, volume 5, pages 127—132.