Обогащённая категория

Пусть ${\displaystyle ({\mathcal {M}},\otimes ,I,\alpha ,\lambda ,\rho )}$ — моноидальная категория. Тогда обогащённая категория ${\displaystyle C}$ над ${\displaystyle {\mathcal {M}}}$ состоит из:

• класса ${\displaystyle Ob(C)}$ — объектов ${\displaystyle {\mathcal {C}}}$,
• объектов ${\displaystyle C(a,b)}$ категории ${\displaystyle {\mathcal {M}}}$ для каждой пары объектов ${\displaystyle a,b\in Ob(C)}$,
• стрелок ${\displaystyle \mathrm {id} _{a}:I\to C(a,a)}$ в ${\displaystyle {\mathcal {M}}}$, выбирающей единицу для каждого объекта ${\displaystyle a\in Ob(C)}$,
• стрелок ${\displaystyle \circ _{abc}:C(b,c)\otimes C(a,b)\to C(a,c)}$ в ${\displaystyle {\mathcal {M}}}$, обозначающей композицию для каждой тройки объектов ${\displaystyle a,b,c\in Ob(C)}$,

с дополнительными свойствами, выражаемыми тремя коммутативными диаграммами. Первая диаграмма обозначает ассоциативность композиции:

Вторая и третья диаграммы соответствуют свойствам единицы:

и

• Обычные категории являются категориями, обогащёнными над ${\displaystyle (\mathbf {Set} ,\times ,\{\cdot \})}$ — категорией множеств с декартовым произведением в качестве моноидальной операции.
• 2-категории — это категории, обогащённые над ${\displaystyle \mathbf {Cat} }$ — категорией малых категорий, с моноидальной структурой, задаваемой произведением категорий.
• Локально конечные категории — это категории, обогащённые над ${\displaystyle (\mathbf {FinSet} ,\times )}$ — категорией конечных множеств с декартовым произведением.
• Предпорядок можно рассматривать как обогащённую категорию над ${\displaystyle \mathbf {2} }$ — категорией из двух элементов и одного морфизма. Категорию ${\displaystyle \mathbf {2} }$ можно интерпретировать как стрелку false → true, тогда моноидальная операция — это конъюнкция, а true — тождественный элемент; паре ${\displaystyle (a,b)}$ сопоставляется true, если ${\displaystyle a\leq b}$. Все необходимые аксиомы следуют из транзитивности и рефлексивности.
• Предаддитивные категории — это категории, обогащённые над ${\displaystyle (\mathbf {Ab} ,\otimes )}$ — категорией абелевых групп с тензорным произведением.

Если существует моноидальный функтор из ${\displaystyle {\mathcal {M}}}$ в ${\displaystyle {\mathcal {N}}}$, то любую категорию, обогащённую над ${\displaystyle {\mathcal {M}}}$, можно рассматривать как категорию, обогащённую над ${\displaystyle {\mathcal {N}}}$. Каждая моноидальная категория ${\displaystyle {\mathcal {M}}}$ имеет моноидальный функтор ${\displaystyle {\mathcal {M}}(I,{\mbox{-}})}$, поэтому в основе любой обогащённой категории лежит обычная категория. Во многих примерах функтор из моноидальной категории в обычную является строгим, и тогда категория, обогащенная над ${\displaystyle {\mathcal {M}}}$, может рассматриваться как обычная категория с добавленной структурой.

Обогащённый функтор — обобщение понятия обычного функтора, а именно, функтор, сохраняющий дополнительную структуру обогащённой категории.

Если ${\displaystyle C}$ и ${\displaystyle D}$ — категории, обогащённые над ${\displaystyle {\mathcal {M}}}$, то ${\displaystyle {\mathcal {M}}}$-обогащённый функтор ${\displaystyle T:C\to D}$ — это отображение, сопоставляющее каждому объекту ${\displaystyle C}$ объект ${\displaystyle D}$ и каждой паре объектов ${\displaystyle a,b\in Ob(C)}$ — морфизм в ${\displaystyle {\mathcal {M}}}$: ${\displaystyle T_{ab}:C(a,b)\to D(T(a),T(b))}$, удовлетворяющий обогащённым версиям свойств функтора. А именно, должна коммутировать диаграмма:

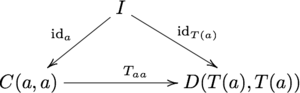
что соответствует уравнению:

${\displaystyle T_{aa}\circ \operatorname {id} _{a}=\operatorname {id} _{T(a)}}$,

где ${\displaystyle I}$ — единица ${\displaystyle {\mathcal {M}}}$. Это аналог свойства обычного функтора ${\displaystyle F(\mathrm {id} _{a})=\mathrm {id} _{F(a)}}$. Также должна коммутировать диаграмма:

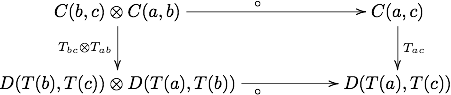
соответствующая правилу: ${\displaystyle F(fg)=F(f)F(g)}$ для обычных функторов.

• Kelly, G.M. Basic Concepts of Enriched Category Theory (англ.) // Reprints in Theory and Applications of Categories. — 2005. — No. 10.
• Маклейн С. Глава 7. Моноиды // Категории для работающего математика = Categories for the working mathematician / Пер. с англ. под ред. В. А. Артамонова. — М.: Физматлит, 2004. — С. 188—221. — 352 с. — ISBN 5-9221-0400-4.

• Lawvere, F.W. Metric Spaces, Generalized Logic, and Closed Categories // Reprints in Theory and Applications of Categories. — 2002. — № 1.