Неравенство Эрдёша — Морделла
Неравенство Эрдёша — Морделла (неравенство Эрдёша — Морделла — Барроу) — планиметрическое утверждение, устанавливает связь между расстояниями от точки внутри треугольника до его сторон с расстояниями от той же точки до вершин треугольника.
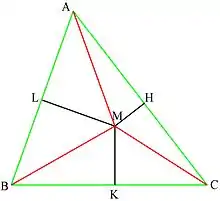
Неравенство Эрдёша — Морделла : MA + MB + MC ≥ 2(MH + MK +ML)
Неравенство
Пусть точка лежит внутри треугольника . Обозначим расстояния от точки до сторон треугольника через , а расстояния от точки до вершин через . Тогда
История
Эрдёш выдвинул это утверждение в качестве гипотезы в 1935 году (Erdős 1935). Через два года доказательство дал Морделл (Mordell & Barrow 1937). Однако его доказательство было весьма сложным. Более простые доказательства даны в (Kazarinoff 1957), (Bankoff 1958) и (Alsina & Nelsen 2007).
Ссылки
- А. Егоров. Треугольники и неравенства // Квант. — 2005. — № 2. — С. 32—33.
- Alsina, Claudi & Nelsen, Roger B. (2007), A visual proof of the Erdős-Mordell inequality, Forum Geometricorum Т. 7: 99–102, <http://forumgeom.fau.edu/FG2007volume7/FG200711index.html> Архивная копия от 16 июля 2020 на Wayback Machine
- Bankoff, Leon (1958), An elementary proof of the Erdős-Mordell theorem, American Mathematical Monthly Т. 65 (7): 521
- Erdős, Paul (1935), Problem 3740, American Mathematical Monthly Т. 42: 396
- Kazarinoff, D. K. (1957), A simple proof of the Erdős-Mordell inequality for triangles, Michigan Mathematical Journal Т. 4 (2): 97–98, DOI 10.1307/mmj/1028988998
- Mordell, L. J. & Barrow, D. F. (1937), Solution to 3740, American Mathematical Monthly Т. 44: 252–254
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.