Наименьший разрез
Наименьший разрез графа — это минимальный в некотором смысле разрез (разбиение вершин графа на два непересекающихся связанных множества).
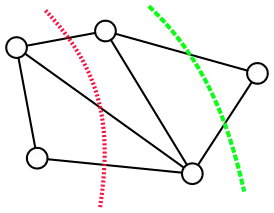
Граф и два его разреза. Красная пунктирная линия представляет разрез из трёх рёбер. Зелёная пунктирная линия представляет один из наименьших разрезов этого графа во втором смысле, состоящий только из двух рёбер. Оба разреза минимальны в первом смысле[1].
Вариации
Вариации наименьшего разреза:
- Разрез с минимальным числом рёбер среди всех разрезов данного разбиения графа на две связные компоненты. Такие разрезы порождают векторное пространство разрезов графа.
- Разрез с минимальным числом рёбер среди всех разрезов в неориентированном графе. Такой разрез определяет рёберную связность графа. Алгоритм Каргера даёт эффективный рандомизированный метод поиска такого разреза.
- Задача о наименьшем разрезе в неориентированных взвешенных графах может быть решена алгоритмом Штёр — Вагнера.
- Обобщение невзвешенного и неориентированного наименьшего разреза, наименьший k-разрез, целью которого является разбиение графа на по меньшей мере k связных компонент путём удаления как можно меньшего числа рёбер.
- Разбиение графа, семейство комбинаторных задач оптимизации, в которых граф разбивается на две или больше частей с дополнительным условием балансировки размеров разреза.
- Разрез потока, который отделяет источник от стока и минимизирует суммарный вес дуг, направленных из части, содержащей источник, в часть, содержащий сток. Как показывает теорема Форда — Фалкерсона, вес такого разреза равен максимальному потоку, который может быть пропущен из источника в сток через данную сеть.
- Разрез взвешенной неориентированной сети, который разделяет выделенную пару вершин и имеет минимальный вес. Система разрезов, которая решает задачу для любой пары вершин, может быть собрана в структуру, известную как дерево Гомори — Ху графа.
Число наименьших разрезов
Граф с n вершинами может иметь не более различных наименьших разрезов.
См. также
- Разрез (теория графов).
- Максимальный разрез графа, который содержит максимально возможное число рёбер
- Вершинный сепаратор, аналогичное понятие, но удаляются вершины, а не рёбра
Примечания
Литература
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.