Модулярность (наука о сетях)

Многие важные научные проблемы могут быть представлены и экспериментально изучены с помощью сетей. Например, биологические и социальные структуры, всемирная паутина, метаболические сети, пищевые сети, нейронные сети и паталогические сети являются проблемами реального мира, которые могут быть математически представлены и изучены топологически для раскрытия некоторых неожиданных структурных свойств[1]. Большинство этих сетей обладают определённой структурой, которая имеет заметную важность для построения и понимания динамики сети. Например, из тесной связанности социального сообщества будет следовать более быстрая передача информации или слухов, чем в случае слабо связанного сообщества. Тогда, если сеть представлена числом индивидуальных узлов, соединённых связями, которые выражают определённую степень взаимосвязи узлов, сообщества определяются как группы тесно взаимодействующих узлов, которые слабо связаны с остальной сетью. Следовательно, может быть крайне важной задачей определить сообщества в сети, поскольку сообщества могут иметь совершенно другие, отличные от средней сети свойства, такие как степень узла, коэффициент кластеризации, степень посредничества, центральность[2] и т.д.. Модулярность является одной из таких мер, максимизация которой приводит к появлению сообществ в данной сети.

Модулярность равна доле рёбер от общего числа рёбер, которые попадают в данные группы минус ожидаемая доля рёбер, которые попали бы в те же группы, если бы они были распределены случайно. Значение модулярности лежит в интервале ${\displaystyle [-1,1]}$[3]. Модулярность положительна, если число рёбер в группах достигает ожидаемого числа. Для данного разбиения узлов сети на некоторые модули модулярность отражает концентрацию связей в модулях по сравнению со случайным распределением связей между всеми узлами без обращения внимания на модули.

Имеются различные методы вычисления модулярности[1]. В наиболее общепринятой версии концепции рандомизация рёбер осуществляется так, что сохраняется степень каждой вершины. Рассмотрим граф с ${\displaystyle n}$ узлами и ${\displaystyle m}$ связями и (рёбрами), такой, что он может быть разбит на два сообщества с помощью переменной ${\displaystyle s}$ членства в сообществах. Если узел ${\displaystyle v}$ принадлежит сообществу 1, ${\displaystyle s_{v}=1}$, а если ${\displaystyle v}$ принадлежит сообществу 2, ${\displaystyle s_{v}=-1}$. Пусть матрица смежности сети представлена матрицей ${\displaystyle A}$, где ${\displaystyle A_{vw}=0}$ означает, что нет ребра (нет связи) между узлами ${\displaystyle v}$ и ${\displaystyle w}$, а ${\displaystyle A_{vw}=1}$ означает, что ребро существует. Также для простоты мы сеть считаем неориентированной. Тогда ${\displaystyle A_{vw}=A_{wv}}$. (Важно заметить, что в общем случае могут существовать кратные рёбра между двумя узлами, но мы принимаем простейший случай).

Модулярность Q определяется как доля рёбер, которые попадают в группу 1 или 2 минус ожидаемое число рёбер в группах 1 и 2 для случайного графа с тем же распределением степеней узлов, как и для данной сети.

Ожидаемое число рёбер может быть вычислено с помощью концепции модели конфигурации[4]. Модель конфигурации является рандомизированной реализацией конкретной сети. Если задана сеть с ${\displaystyle n}$ узлами, в которой каждый узел ${\displaystyle v}$ имеет степень ${\displaystyle k_{v}}$, модель конфигурации рассекает каждое ребро на две половинки, а затем каждая половинка ребра, называемая обрубком, соединяется случайным образом с любым другим обрубком сети (за исключением себя), даже позволяя петли (что случается, когда обрубок соединяется с другим обрубком в том же самом узле) и кратные рёбра между той же самой парой узлов. Тогда, даже при сохранении степени узла графа, модель конфигурации приводит к совершенно случайной сети.

Рассмотрим теперь два узла v и w со степенями ${\displaystyle k_{v}}$ и ${\displaystyle k_{w}}$ соответственно из случайно перемещённых связей, как описано выше. Мы вычисляем ожидаемое число полных рёбер между этими узлами.

Пусть общее число обрубков в сети будет ${\displaystyle l}$:

${\displaystyle l=\sum _{u}k_{u}=2m}$

(1)

Рассмотрим каждый из ${\displaystyle k_{v}}$ обрубков узла v и создадим ассоциативные индикаторные переменные ${\displaystyle I_{i}}$ для них, ${\displaystyle i=1,\ldots ,k_{v}}$, с ${\displaystyle I_{i}=1}$, если i-ый обрубок оказывается связанным с одним из ${\displaystyle k_{w}}$ обрубков узла w в этом случайном графе. Если нет, значение равно 0. Поскольку i-ый обрубок узла v может быть соединён с любым из ${\displaystyle 2m-1}$ оставшихся обрубков с равной вероятностью и поскольку имеется ${\displaystyle k_{w}}$ обрубков, которые ассоциированы с узлом w, очевидно, что

${\displaystyle p(I_{i}=1)=E[I_{i}]={\frac {k_{w}}{2m-1}}}$

Общее число полных рёбер ${\displaystyle J_{vw}}$ между узлами v и w тогда равно ${\displaystyle J_{vw}=\sum _{i}^{k_{v}}I_{i}}$, так что ожидаемое значение равно

${\displaystyle E[J_{vw}]=E[\sum _{i}I_{i}]=\sum _{i}^{k_{v}}E[I_{i}]={\frac {k_{v}k_{w}}{2m-1}}}$

Во многих статьях делается следующее приближение для случайных сетей с большим числом рёбер. Если m велико, отбрасывается вычитание единицы из знаменателя в формуле выше и просто используется более простое приближённое выражение ${\displaystyle {\frac {k_{v}k_{w}}{2m}}}$ для ожидаемого числа рёбер между двумя узлами. Кроме того, в большой случайной сети число петель и кратных рёбер исчезающе мало. Игнорирование петель и кратных рёбер позволяет предположить, что имеется максимум одно ребро между двумя узлами. В этом случае ${\displaystyle J_{vw}}$ становится двоичной индикаторной переменной, так что её ожидаемое значение равно вероятности, что переменная примет значение 1, это означает, что вероятность ребра между узлами v и w можно приблизительно считать равной ${\displaystyle {\frac {k_{v}k_{w}}{2m}}}$.

Таким образом, разность между действительным числом рёбер между узлами ${\displaystyle v}$ и ${\displaystyle w}$ и ожидаемым числом рёбер между ними равно

${\displaystyle A_{vw}-{\frac {k_{v}k_{w}}{2m}}}$

Суммирование по всем парам даёт уравнение для модулярности ${\displaystyle Q}$[1].

${\displaystyle Q={\frac {1}{2m}}\sum _{vw}\left[A_{vw}-{\frac {k_{v}k_{w}}{2m}}\right]{\frac {s_{v}s_{w}+1}{2}}}$

(3)

Важно заметить, что Ур. 3 хорошо выполняется только для разбиения на два сообщества. С помощью иерархического разбиения (например, разбиение на два сообщества, затем два подсообщества разбиваются на два меньших подсообщества для максимизации Q) можно приблизиться к выявлению любого числа сообществ в сети. Кроме того, (3) может быть обобщено до разбиения сети на c сообществ[5].

${\displaystyle Q={\frac {1}{(2m)}}\sum _{vw}\left[A_{vw}-{\frac {k_{v}k_{w}}{(2m)}}\right]\delta (c_{v},c_{w})=\sum _{i=1}^{c}(e_{ii}-a_{i}^{2})}$

(4)

,

где e_ij является долей рёбер с одним концом в сообществе i и другим в сообществе j:

${\displaystyle e_{ij}=\sum _{vw}{\frac {A_{vw}}{2m}}1_{v\in c_{i}}1_{w\in c_{j}}}$

а a_i является долей концов рёбер, которые соединены с вершинами в сообществе i:

${\displaystyle a_{i}={\frac {k_{i}}{2m}}=\sum _{j}e_{ij}}$

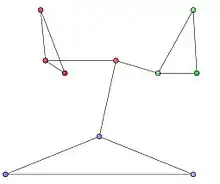
Мы рассмотрим неориентированную сеть с 10 узлами и 12 рёбрами и следующей матрицей смежности.

Рис. 1. Сеть, соответствующая матрице смежности с 10 узлами и 12 рёбрами.

Рис. 2. Разбиение сети, которое максимизирует Q. Максимальное значение Q=0,4896

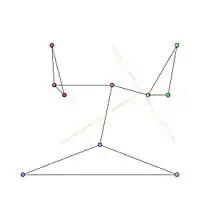
Сообщества в графе представлены красными, зелёными и синими узлами кластеров на рис. Fig 1. Оптимальное разбиение на сообщества представлено на рис. 2.

Альтернативная формулировка модулярности, полезная, в частности, в алгоритмах спектральной оптимизации, следующая[1]. Определим ${\displaystyle S_{vr}}$ равной 1, если вершина v принадлежит группе r, и равной нулю в противном случае. Тогда

${\displaystyle \delta (c_{v},c_{w})=\sum _{r}S_{vr}S_{wr}}$,

а следовательно,

${\displaystyle Q={\frac {1}{2m}}\sum _{vw}\sum _{r}\left[A_{vw}-{\frac {k_{v}k_{w}}{2m}}\right]S_{vr}S_{wr}={\frac {1}{2m}}\mathrm {Tr} (\mathbf {S} ^{\mathrm {T} }\mathbf {BS} ),}$

где S является (не квадратной) матрицей, имеющей элементы ${\displaystyle S_{vr}}$, а B является так называемой матрицей модулярности, которая имеет элементы

${\displaystyle B_{vw}=A_{vw}-{\frac {k_{v}k_{w}}{2m}}.}$

Все строки и столбцы матрицы модулярности в сумме дают нуль, что означает, что модулярность неразделённой сети всегда равна нулю.

Для сетей, разбитых на два сообщества, можно определить ${\displaystyle s_{v}=\pm 1}$, для того чтобы показать, какому сообществу принадлежит узел v, что приводит к

${\displaystyle Q={1 \over 4m}\sum _{vw}B_{vw}s_{v}s_{w}={1 \over 4m}\mathbf {s} ^{\mathrm {T} }\mathbf {Bs} ,}$

где s является вектор-столбцом с элементами ${\displaystyle s_{v}}$[1].

Эта функция имеет тот же вид, что и гамильтониан спинового стекла Изинга, который используется для создания простых компьютерных алгоритмов, например, используя имитацию отжига, для максимизации модулярности. Общая форма модулярности для произвольного числа сообществ эквивалентна спиновым стёклам Поттса и аналогичные алгоритмы могут быть разработаны также и в этом случае[6].

Модулярность сравнивает число рёбер внутри кластера с ожидаемым числом рёбер, которые находились бы в кластере, если бы сеть была случайной сетью с тем же числом узлов, в которой каждый узел сохраняет свою степень, но рёбра соединяют узлы случайным образом. Эта модель случайного графа (null model) явно предполагает, что каждый узел может быть присоединён к любому другому узлу сети. Это предположение, однако, нецелесообразно, если сеть очень велика, так как горизонт узла включает малую часть сети, игнорируя большую часть сети. Однако из этого следует, что ожидаемое число рёбер между двумя группами узлов уменьшается, если размер сети возрастает. Таким образом, если сеть достаточно велика, ожидаемое число рёбер между двумя группами узлов в модулярности модели случайного графа может быть меньше единицы. Если это происходит, отдельное ребро между двумя кластерами можно было бы интерпретировать с оглядкой на модулярность как признак сильной корреляции между двумя кластерами, а оптимизация модулярности привела бы к слиянию двух кластеров независимо от свойств кластеров. Таким образом, даже слабо связанные полные графы, которые имеют высокую возможную плотность внутренних рёбер и представляют хорошо распознаваемые сообщества, могли бы быть слиты путём оптимизации модулярности, если бы сеть была достаточно велика[7]. По этой причине оптимизация модулярности в больших сетях не смогла бы распознать малые сообщества, даже когда они хорошо определены. Эта тенденция неизбежна для методов типа оптимизации модулярности, которые опираются на глобальной модели случайного графа[8].

Имеется два главных подхода, которые пытаются решить проблему разрешающей способности в контексте модулярности — добавление сопротивления r в каждый узел в виде петли, которое увеличивает (${\displaystyle r>0}$) или уменьшает (${\displaystyle r<0}$) желание узлов формировать сообщества[9], или добавление параметра ${\displaystyle \gamma >0}$ перед членом случайного графа в определении модулярности, которые определяют относительную важность между внутренними связями сообществ и моделью случайного графа[6]. Оптимизация модулярности для значений этих параметров в их соответствующих подходящих интервалах, позволяет обнаружить полный мезомасштаб сети от мезомасштаба, в котором все узлы принадлежат одному сообществу, до микромасштаба, в которой любой узел образует собственное сообщество, откуда и название методы мультиразрешения. Однако было показано, что эти методы имеют ограничения, когда сообщества очень различаются в размерах[10].

• Сложные сети
• Структура сообщества