Метод Касиски
Метод Каси́ски (Метод Кази́ского) — метод криптоанализа полиалфавитных шифров, таких как шифр Виженера. Основан на факте того, что повторяющиеся части открытого текста, зашифрованные одним и тем же ключевым словом, приводят к идентичным сегментам шифрованного текста.[1] Разработан независимо криптоаналитиками Фридрихом Касиски и Чарльзом Бэббиджем.
История
В 1863 году Фридрих Вильгельм Касиски опубликовал свой 95-страничный труд «Die Geheimschriften und die Dechiffrirkunst»(«Тайнопись и искусство дешифрирования», оригинал рукописи находится в библиотеке в Мюнхене). Это была книга об атаках на шифры, созданные с помощью полиалфавитной замены. В этой книге Касиски описывает своё крупное открытие в криптоанализе, а именно — алгоритм, известный всем как «Тест Касиски»[2] или «Тест Казисского»[3]. Этот алгоритм позволял взламывать шифр Виженера, взлом которого считался невозможным на протяжении 400 лет. Открытие Касиски уступает по важности только работе Аль-Кинди, известного как «философ арабского мира».[4], который открыл метод частотного анализа для дешифрования текста.
Однако за десять лет до Касиски успеха во взломе шифра Вижинера добился Чарльз Бэббидж. Бэббидж сделал своё открытие в 1854 году, но о нём так никто и не узнал, потому что Бэббидж так и не опубликовал его. Это обнаружилось только в двадцатом веке, когда ученые принялись разбирать его многочисленные заметки. Так почему же Бэббидж не сообщил о том, что сумел взломать этот имеющий столь важное значение шифр? Несомненно, была у него такая привычка — бросать незавершенными значительные и многообещающие начинания и не сообщать о своих открытиях. Имеется, однако, и другое объяснение. Бэббидж сделал своё открытие вскоре после того, как разразилась Крымская война, и в одной из теорий было выдвинуто предположение, что оно давало Британии явное преимущество над Россией, её противником. Вполне возможно, что британская секретная служба потребовала от Бэббиджа сохранить свою работу в секрете, тем самым обеспечив себе девятилетнюю фору перед остальным миром.[2] Так или иначе, взлом шифра Виженера закреплен за Касиски. «Метод Касиски» открыл путь и к другим полиалфавитным решениям, которые до сих пор используют правительства разных стран. Его труд признан величайшей книгой криптологии.
Достижения Чарльза Бэббиджа и Фридриха Касиски показали, что шифр Виженера небезопасен. Это открытие повлекло смятение у криптографов того времени, ведь они теперь не могли гарантировать секретность. И почти на полвека криптоанализ обрел контроль в коммуникационной войне. Криптографы не могли придумать ничего нового, что повлекло рост интереса у широкой публики к шифрам. В конце концов был найден шифр на замену шифра Виженера — так называемый шифр Бейла.[2]
Идея
Идея метода основана на том, что ключи являются периодическими, а в естественном языке существуют часто встречающиеся буквосочетания: биграммы и триграммы. Это наводит на мысль, что повторяющиеся наборы символов в шифротексте — повторения популярных биграмм и триграмм исходного текста.
Метод Касиски позволяет криптоаналитику найти длину ключевого слова, используемого в полиалфавитном шифре. Как только длина ключевого слова обнаружена, криптоаналитик выстраивает зашифрованный текст в n колонках, где n — длина ключевого слова. Тогда каждую колонку можно рассматривать как зашифрованный моноалфавитным шифром текст, который можно подвергнуть частотному анализу.
Метод Касиски заключается в поиске групп символов, которые повторяются в зашифрованном тексте. Группы должны состоять из не менее чем трех символов. Тогда расстояния между последовательными возникновениями групп, вероятно, будут кратны длине ключевого слова. Предполагаемая длина ключевого слова кратна наибольшему общему делителю всех расстояний.
Причина, по которой метод работает — это то, что если две группы символов повторяются в исходном тексте и расстояние между ними является кратным длине ключевого слова, то буквы ключевого слова выровняются с обеими группами.
Описание
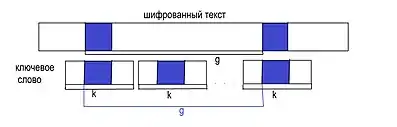
Если повторяющаяся подстрока в открытом тексте зашифровывается одной и той же подстрокой в ключевом слове, тогда шифрованный текст содержит повторяющуюся подстроку, а расстояние между двумя вхождениями кратно длине ключевого слова.
Расстояние между двумя повторяющимися подстроками в зашифрованном тексте g. Ключевое слово длиной k повторяется, чтобы заполнить длину зашифрованного текста, расстояние g кратно длине ключевого слова k. Таким образом, если мы видим две повторяющиеся подстроки с расстоянием g, то один из делителей g может быть длиной ключевого слова. Например, если расстояние равно g = 18, поскольку делители g равны 2, 3, 6, 9 и 18, один из них может быть длиной неизвестного ключевого слова.[5]
Свойства
Сложность метода Касиски состоит в необходимости поиска повторяющихся строк. Это сложно сделать вручную, но значительно проще на компьютере. Однако метод требует вмешательства человека, так как некоторые совпадения могут оказаться случайными, что приведет к тому, что наибольший общий делитель всех расстояний будет равен 1. Криптоаналитик должен выяснить, какие длины являются подходящими. И, в конечном итоге, человек должен проверить правильность подобранного периода исходя из осмысленности расшифрованного текста.
Применение
Несмотря на свою слабость, метод Касиски использовался в качестве вспомогательного во Второй мировой войне.
Было построено специальное устройство для определения совпадений в тексте и расстояния между ними. Устройство работало с пятью лентами, замыкающимися в петлю, и могло находить повторяющиеся биграммы и триграммы в тексте.
Устройство было довольно быстрым: для обработки набора 10 000 символов, требовалось менее трех часов. Оно служило в основном для получения быстрой информации о текстах, которые были зашифрованы одним и тем же ключом. Устройство было уничтожено в конце войны.[6]
Примеры
Пример 1
Рассмотрим следующий пример, зашифрованный ключевым словом ION. Подстрока BVR в зашифрованном тексте повторяется три раза. Первые два зашифрованы с помощью ION. Так как ключевое слово ION сдвигается вправо несколько раз, расстояние между B в первом вхождении BVR и вторым кратно длине ключевого слова 3. Второе и третье вхождения BVR зашифровываются как THE и NIJ, используя разные части ключевого слова (то есть ION и ONI), а расстояние между двумя B во втором и третьем BVR может не быть кратным длине ключевого слова. Поэтому даже мы находим повторяющиеся подстроки, расстояние между ними может быть или не быть кратным длине ключевого слова, а повторения могут быть просто случайными.
| Текст | ......THE................THE.....................NIJ........... |
| Ключевое слово | ......ION................ION....................IONI........... |
| Зашифрованный текст | ......BVR................BVR.....................BVR........... |
Пример 2
В длинном зашифрованном тексте больше шансов найти повторяющиеся подстроки. Короткий текст, зашифрованный относительно длинным ключевым словом, может создать зашифрованный текст, в котором не будет повторения. Кроме того, подстроки, повторяющиеся много раз, в зашифрованном тексте вряд ли будут случайными, тогда как короткие повторные подстроки могут появляться чаще и некоторые из них могут быть исключительно случайными. В данном примере показано шифрование Michigan Technological University с ключевым словом boy. Нет повторной подстроки длиной не менее 2. В данном случае метод Касиски терпит неудачу.
| MICHI GANTE CHNOL OGICA LUNIV ERSIT Y |
| BOYBO YBOYB OYBOY BOYBO YBOYB OYBOY B |
| NWAIW EBBRF QFOCJ PUGDO JVBGW SPTWR Z |
Пример 3
Рассмотрим более длинный открытый текст. Ниже приводится цитата Чарльза Энтони Ричарда, победителя премии ACM Turing 1980 года по разработке программного обеспечения:
| There are two ways of constructing a software design: |
| One way is to make it so simple that there are obviously |
| no deficiencies, and the other way is to make it so complicated |
| that there are no obvious deficiencies. |
| The first method is far more difficult. |
После удаления пробелов и пунктуации и преобразования в верхний регистр получается следующее:
| THERE ARETW OWAYS OFCON STRUC TINGA SOFTW AREDE SIGNO NEWAY |
| ISTOM AKEIT SOSIM PLETH ATTHE REARE OBVIO USLYN ODEFI CIENC |
| IESAN DTHEO THERW AYIST OMAKE ITSOC OMPLI CATED THATT HEREA |
| RENOO BVIOU SDEFI CIENC IESTH EFIRS TMETH ODISF ARMOR EDIFF |
| ICULT |
Затем полученный текст шифруется с помощью 6 буквенного ключевого слова SYSTEM следующим образом:
| LFWKI MJCLP SISWK HJOGL KMVGU RAGKM KMXMA MJCVX WUYLG GIISW |
| ALXAE YCXMF KMKBQ BDCLA EFLFW KIMJC GUZUG SKECZ GBWYM OACFV |
| MQKYF WXTWM LAIDO YQBWF GKSDI ULQGV SYHJA VEFWB LAEFL FWKIM |
| JCFHS NNGGN WPWDA VMQFA AXWFZ CXBVE LKWML AVGKY EDEMJ XHUXD |
| AVYXL |
Сравним текст, ключевое слова и зашифрованный текста. Выделенный в таблице текст означает повторяющиеся подстроки длиной 8. Это самые длинные подстроки длиной менее 10 в зашифрованном тексте. Строка открытого текста THEREARE появляется три раза в позициях 0, 72 и 144. Расстояние между двумя вхождениями равно 72. Повторяющееся ключевое слово и зашифрованный текст представляют собой SYSTEMSY и LFWKIMJC соответственно. Следовательно, эти три события не случайны, а 72 кратно длине ключевого слова 6.
| THERE ARETW OWAYS OFCON STRUC TINGA SOFTW AREDE SIGNO NEWAY |
| SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY |
| LFWKI MJCLP SISWK HJOGL KMVGU RAGKM KMXMA MJCVX WUYLG GIISW |
| ISTOM AKEIT SOSIM PLETH ATTHE REARE OBVIO USLYN ODEFI CIENC |
| STEMS YSTEM SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST |
| ALXAE YCXMF KMKBQ BDCLA EFLFW KIMJC GUZUG SKECZ GBWYM OACFV |
| IESAN DTHEO THERW AYIST OMAKE ITSOC OMPLI CATED THATT HEREA |
| EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY STEMS YSTEM |
| MQKYF WXTWM LAIDO YQBWF GKSDI ULQGV SYHJA VEFWB LAEFL FWKIM |
| RENOO BVIOU SDEFI CIENC IESTH EFIRS TMETH ODISF ARMOR EDIFF |
| SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY |
| JCFHS NNGGN WPWDA VMQFA AXWFZ CXBVE LKWML AVGKY EDEMJ XHUXD |
| ICULT |
| STEMS |
| AVYXL |
Следующая самая длинная повторяющаяся подстрока WMLA в зашифрованном тексте имеет длину 4 и встречается в положениях 108 и 182. Расстояние между этими двумя положениями равно 74. В позиции 108 не зашифрованный EOTH зашифрован для WMLA с использованием SYST. В позиции 182 открытый текст ETHO шифруется WMLA с использованием STEM. В этом случае, даже если мы найдем повторяющиеся подстроки WMLA, они не зашифрованы одной и той же частью ключевого слова, и они поступают из разных разделов открытого текста. В результате это повторение является чистой случайностью, и расстояние 74 вряд ли будет кратным длине ключевого слова.
| IESAN DTHEO THERW AYIST OMAKE ITSOC OMPLI CATED THATT HEREA |
| EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY STEMS YSTEM |
| MQKYF WXTWM LAIDO YQBWF GKSDI ULQGV SYHJA VEFWB LAEFL FWKIM |
| RENOO BVIOU SDEFI CIENC IESTH EFIRS TMETH ODISF ARMOR EDIFF |
| SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY |
| JCFHS NNGGN WPWDA VMQFA AXWFZ CXBVE LKWML AVGKY EDEMJ XHUXD |
| ICULT |
| STEMS |
| AVYXL |
Существует пять повторяющихся подстрок длины 3. Они являются MJC в положениях 5 и 35 с расстоянием 30, ISW в позициях 11 и 47 (расстояние = 36), KMK в положениях 28 и 60 (расстояние = 32), VMQ в положениях 99 и 165 (расстояние = 66) и DAV в положениях 163 и 199 (расстояние = 36). Следующая таблица представляет собой сводку. Повторяющийся зашифрованный текст KWK зашифрован из двух разделов открытого текста GAS и SOS с частями ключевого слова EMS и SYS, соответственно. Поэтому это чистый шанс.
| Позиция | 5 | 35 | 11 | 47 | 28 | 60 | 99 | 165 | 163 | 199 |
| Расстояние | 30 | 36 | 32 | 66 | 36 | |||||
| Текст | ARE | ARE | WAY | WAY | GAS | SOS | CIE | CIE | FIC | FIC |
| Ключевое слово | MSY | MSY | MSY | MSY | EMS | SYS | TEM | TEM | YST | YST |
| Шифрованный текст | MJC | MJC | ISW | ISW | KMK | KMK | VMQ | VMQ | DAV | DAV |
В следующей таблице указаны расстояния и их факторы. Поскольку расстояние может быть кратным длине ключевого слова, фактором расстояния может быть длина ключевого слова. Если совпадение по чистой случайности, факторы этого расстояния могут не быть факторами длины ключевого слова. В общем, хороший выбор - самый большой, который появляется чаще всего. Более длинные повторяющиеся подстроки могут предлагать лучший выбор, потому что эти совпадения с меньшей вероятностью случайны.
| Длина | Расстояние | Факторы |
| 8 | 72 | 2 3 4 6 8 9 12 18 24 36 72 |
| 4 | 74 | 2 37 74 |
| 3 | 66 | 2 3 6 11 22 33 66 |
| 36 | 2 3 4 6 9 12 18 36 | |
| 32 | 2 4 8 16 32 | |
| 30 | 2 3 5 6 10 15 |
В следующей таблице указаны расстояния и все факторы, не превышающие 20. Последняя строка таблицы имеет общее количество каждого фактора. Ясно, что факторы 2, 3 и 6 встречаются чаще всего со счетами 6, 4 и 4 соответственно. Поскольку длина ключевого слова 2 слишком мала, чтобы эффективно использоваться, длины 3 и 6 более разумны. В результате мы можем использовать 3 и 6 в качестве исходных оценок для восстановления ключевого слова и расшифровки зашифрованного текста.
| Факторы | |||||||||||||||||||
| Расстояния | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 74 | X | ||||||||||||||||||
| 72 | X | X | X | X | X | X | X | X | |||||||||||
| 66 | X | X | X | X | |||||||||||||||
| 36 | X | X | X | X | X | X | X | ||||||||||||
| 32 | X | X | X | X | |||||||||||||||
| 30 | X | X | X | X | X | X | |||||||||||||
| Сумма | 6 | 4 | 3 | 1 | 4 | 0 | 2 | 2 | 1 | 1 | 2 | 0 | 0 | 1 | 1 | 0 | 2 | 0 | 0 |
Если мы убеждены, что некоторые расстояния, вероятно, не будут случайными, мы можем вычислить наибольший общий делитель (НОД) этих расстояний и использовать его как возможную длину ключевого слова. Как упоминалось ранее, расстояния 74 и 32 могут быть случайными, а оставшиеся расстояния равны 72, 66, 36 и 30. Их НОД - это НОД(72, 66, 36, 30) = 6. Поскольку мы знаем ключевое слово SYSTEM, 6 - правильная длина. Если у нас есть только зашифрованный текст, мы должны выполнить некоторые предположения.
| Так как НОД(a,b,c,d) = НОД(НОД(a,b),c,d), имеем НОД(72,66,36,30) = НОД(НОД(72,66),36,30) = НОД(6,36,30) = НОД(НОД(6,36),30) = НОД(6,30) = 6 |
Пример 4
Шифрование полиалфавитным шифром с периодом 4
Пусть шифруется следующий текст. Шифрование происходит без учета знаков препинания и различия строчных и прописных букв. Пробелы оставлены в тексте, чтобы его удобно было читать, при шифровании же пробелы были опущены:[7]
Игры различаются по содержанию характерным особенностям а также по тому какое место они занимают в жизни детей их воспитании и обучении Каждый отдельный вид игры имеет многочисленные варианты Дети очень изобретательны Они усложняют и упрощают известные игры придумывают новые правила и детали Например сюжетно ролевые игры создаются самими детьми но при некотором руководстве воспитателя Их основой является самодеятельность Такие игры иногда называют творческими сюжетно ролевыми играми Разновидностью сюжетно ролевой игры являются строительные игры и игры драматизации В практике воспитания нашли своё место и игры с правилами которые создаются для детей взрослыми К ним относятся дидактические подвижные и игры забавы В основе их лежит четко определённое программное содержание дидактические задачи и целенаправленное обучение. Для хорошо организованной жизни детей в детском саду необходимо разнообразие игр так как только при этих условиях будет обеспечена детям возможность интересной и содержательной деятельности Многообразие типов видов форм игр неизбежно как неизбежно многообразие жизни которую они отражают как неизбежно многообразие несмотря на внешнюю схожесть игр одного типа модели
Воспользуемся полиалфавитным шифром с периодом 4:
АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ - чистый алфавит ЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИ - 1-й алфавит ГАЭЪЧФСОЛИЕВЯЬЩЦУРНКЗДБЮЫШХТПМЙЖ - 2-й алфавит БФЗЪНАУЖЩМЯТЕШЛЮСДЧКЭРГЦЙЬПВХИЫО - 3-й алфавит ПЪЕРЫЖСЬЗТЭИУЮЙФЯКХАЛЦБМЧВНШГОЩД - 4-й алфавит
Зашифрованное сообщение:
СЪСШ ЩГЖИСЮБЩЫРО ФЧ РЛЫОУУПЦЛЫ ЦЙУБЭЫФСЮДЯ ЛКЧААЮЦЩДХИЯ Б ХЙЕУЖ ШЩ ЧЙХК ЯПУЩА УОРЧЙ ЧЬЩ ЬЙЬЩУЙЙЧ Е ПЛЖЮС ЧАХОИ ЩЦ ЛЩДФСНБЮСЛ Щ ЙККЦЖЦЛЩ ЭЙСНШТ ЩЧЫОВХЮДИ ЗЗН ЛЪЯД ЛЕЖОН ЕЮЧЪЛМСРТЖЦЬВЖ ЛГСЗЙЬЧШ НФЧЗ ЧЮАЮЕ ЛЖЙКУАХЙНАИЕЬВ ЙЦЛ ККФЩУЮИЙЧ З ЬЦСЙВГЫХ СОЗЖЪНШШО ЛЪЯД ЦСЗНКЕШЛГЫХ ЦЩЗШО ЦСПЛЛТП С ЧАХЙВЩ ЮЙЦСЗХФС КЗСАХЦЩ СЙФФЗШО ЛЪЯД РЛЬНГЫХЪЖ ДПХЛЕЗ НФЧГХЛ ШЙ ШУЩ ЮОЕЛХЧУЛУ ЩКЯЙЛЩНКЫЭА ЕЧРЮЗЫГЧЖФЖ ЩЦ ЧРШЙЛЩМ ДЛВОЖЫРО КЙЯЛЫОЖЧЖФПШЙЪНХ ХЙЕЩЖ СЪСШ СЬЛРНГ ШПРТЗПЗН ЧЕЧУЦЖЪЕЩУС РЫСОНШЙ ЩЩТЖЛТЕЗ СЪСПХЛ СПРЬЛЕСЧШЙЪНХЩ ЪЙУЖЫЬЛ ЯЧВАЕЧИ ЩРЩТ ОЕФЖЫХЪЖ ДХЩЩЩХОВХЮДФ ЩРЩТ Щ ЗМУВ ЫЩГЕПЫЛЖПЯЛЩ Е ШУБЭЫЛЯЖ ЛЩДФСНБЮСЖ ШПБВЩ КЛЩА УОРЧЙ С ЛЪЯД Р ЮЯЙЭЩИЙЯЩ ЭЧНЛЯДФ ДЙРЧБЩЫРО ЫФЖ НЖЫФМ ЕРУЛКФТЕЗ У ЬЩУ ЧНШЙЪЖЧКИ ЧЩЫЙЕЧЗАФДЭСФ ЮЙНЭЩСЦТА З СЪСШ РГФПЛТ З ЙЪЬЛЕО ЛР ИОСЩХ АФЧЭЧ ЩЮЯОЧАИОЬШЙО ЦСЙМУБУХЬЛЖ ЪЩНЖЩСБЮСФ НЗНГЯХСЮАКУЛА ЬЙЧБМС Л ГЖФФШПШУБЕФФШЮЧФ ЛЪЬЮАЮСФ НИИ ДЛЯЧЫЛ ЙЩЪБЮСОЛЕЙЬШЙТ СЩЬЦЛ НЖЫФМ Е НФЧКУЩЕ КЙЧК ЮОЩФЦЧЧЩУЧ УБЬЦЩЛЪЩГЖЗО ЛЪЯ ЫГЯ ЭЙЕ ЧЙФПЯЙ ШУЩ ОЫЛР АЪВЛЕСЖР ЪЬЧАХ ЧААКШФЦЖЦГ НЖЫЖЕ ЕЧОЕЙПЬЛКЫП ЩЮЫФСЖЪЬЛТ С РЛЫОУУПЫФТГЦЩМ ЫОЖЧЖФПШЙЪНЩ УЦЩЪЙЧАСПРЛА ХСЦЛЕ ЛЛНЙЛ ЗЛЯХ ЛЪЯ ЦФЩЬКФУЮЧ ЕБЭ ЦФЩЬКФУЮЧ ЯШЙМЩЛЪЩГЖЗО СЩЬЦЛ ЯЙЫЩСАЗ ЩШЗ ЧНСППГЫХ УГЯ ЮОЛЖЪОСШЙ ХЬЛРЧЩФЯЙОЩЖ ЦФДУЧНСД ЦГ ЗЮОЫШЩЗ РРЙПФДХЕ ЛЪЯ ЧЧШЙМЩ ЧЗШГ ЕЙНФТЗ
Воспользуемся методом Касиски для того, чтобы расшифровать это сообщение. Но предварительно подсчитаем число появлений каждой буквы в шифротексте. Эти данные приведем в таблице, где i в первой строке означает букву алфавита, а fi во второй строке — это число появлений этой буквы в шифротексте. Всего в нашем шифротексте имеется L = 1036 букв.
| i | А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П |
| fi | 26 | 15 | 11 | 21 | 20 | 36 | 42 | 31 | 13 | 56 | 23 | 70 | 10 | 33 | 36 | 25 |
| i | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ъ | Ы | Ь | Э | Ю | Я |
| fi | 28 | 54 | 15 | 36 | 45 | 32 | 31 | 57 | 35 | 72 | 32 | 35 | 27 | 11 | 30 | 28 |
- Группа СЪС встречается в позициях 1, 373, 417, 613. Соответствующие расстояния равны
373 — 1 = 372 = 4 * 3 * 31
417—373 = 44 = 4 * 11
613—417 = 196 = 4 * 49.
Наибольший общий делитель равен 4. Делаем вывод, что период кратен 4.
- Группа ЩГЖ встречается в позициях 5, 781, 941. Соответствующие расстояния равны
781 — 5 = 776 = 8 * 97
941—781 = 160 = 32 * 5.
Делаем вывод, что период кратен 8, что не противоречит выводу для предыдущей группы (кратен 4).
- Группа ЫРО встречается в позициях 13, 349, 557. Соответствующие расстояния равны
349 — 13 = 336 = 16 * 3 * 7
557—349 = 208 = 16 * 13.
Делаем вывод, что период кратен 4.
Правдоподобным является предположение, что период равен 4.
Далее текст подвергается частотному анализу.
Пример 5
Шифрование с помощью секретного слова
Посмотрим на следующий зашифрованный текст:[8]
UTPDHUG NYH USVKCG МУСЕ FXL KQIB. WX RKU GI TZN, RLS BHZLXMSNP KDKS; СЕВ Ш HKEWIBA, YYM SRB PER SBS, JV UPL О UVADGR HRRWXF. JV ZTVOOV УН ZCQU У UKWGEB, PL UQFB Р FOUKCG, TBF RQ VHCF R KPG, 0U КЕТ ZCQU MAW QKKW ZGSY, ЕР PGM QKETK UQEB DER EZRN, MCYE, MG UCTESVA, WP КЕТ ZCQU MAW KOIJS, LCOV NTHDNV JPNUJVB Ш GGV RWX ONKCGTHKFL XG VKD, ZJM VG CCI MVGD JPNUJ, RLS EWVKJT ASGUCS MVGD; DDK VG NYH PWUV CCHIIY RD DBQN RWTH PFRWBBI VTTK VCGNTGSF FL IAWU XJDUS, HFP VHSF, RR LAWEY QDFS RVMEES FZB СНН JRTT MVGZP UBZN FD ATIIYRTK WP КЕТ HIVJCI; TBF BLDPWPX RWTH ULAW TG VYCHX KQLJS US DCGCW OPPUPR, VG KFDNUJK GI JIKKC PL KGCJ lAOV KFTR GJFSAW KTZLZES WG RWXWT VWTL WP XPXGG, CJ EPOS VYC BTZCUW XG ZGJQ PMHTRAIBJG WMGEG. JZQ DPB JVYGM ZCLEWXR:CEB lAOV NYH JIKKC TGCWXE UHE JZK. WX VCULD YTTKETK WPKCGVCWIQT PWVY QEBFKKQ, QNH NZTTWIREL IAS VERPE ODJRXGSPTC EKWPTGEES, GMCG TTVVPLTEEJ; YCW WV NYH TZYRWH LOKU MU AWO, KEPM VG BLTP VQN RD DSGG AWKWUKKPL KGCJ, XY GPP KPG ONZTT ICUJCHLSE KET DBQHJTWUG. DYN MVCK ZT MEWCW HTWE ED JL, GPU YAE CH LQ! PGR UE, YH MWPP RXE CDJCGOSE, XMS UZGJQJL, SXVPN HBG!
Исследуем расстояния между сочетаниями WX. Некоторые из расстояний равны 9, 21, 66, 30. Какие-то совпадения могут оказаться случайными, а какие-то содержат информацию о длине ключа. Вычислим НОД (попарно):
НОД(30,66) = 6
НОД(9,66) = 3
НОД(9,30) = 3
НОД(21,66) = 3
Однако, маловероятно, что длина состоит всего лишь из трех букв, поэтому предположим числа 9 и 21 случайными и будем считать длину ключа равной 6.
Далее берется каждая шестая буква шифротекста и применяется частотный анализ — определяется первая буква ключа, за ней вторая и так далее. Определение буквы происходит с помощью построения гистограммы. Сравниваем частоту повторяемости каждой шестой буквы, начиная с первой, со среднестатистической (см. рисунок). Таким образом находим, что ключевое слово «crypto».
Исходный текст (отрывок из произведения Чарльза Диккенса «Рождественская песнь в прозе. Святочный рассказ с привидениями»):
Scrooge was better than his word. He did it all, and infinitely more; and to Tiny Tim, who did not die, he was a second father. He became as good a friend, as good a master, and as good a man, as the good old city knew, or any other good old city, town, or borough, in the good old world. Some people laughed to see the alteration in him, but he let them laugh, and little heeded them; for he was wise enough to know that nothing ever happened on this globe, for good, at which some people did not have their fill of laughter in the outset; and knowing that such as these would be blind anyway, he thought it quite as well that they should wrinkle up their eyes in grins, as have the malady in less attractive forms. His own heart laughed: and that was quite enough for him. He had no further intercourse with Spirits, but lived upon the Total Abstinence Principle, ever afterwards; and it was always said of him, that he knew how to keep Christmas well, if any man alive possessed the knowledge. May that be truly said of us, and all of us! And so, as Tiny Tim observed, God bless Us, Every One!
См. также
Примечания
- Menezes, A. J. (Alfred J.), 1965-. Handbook of applied cryptography. — Boca Raton: CRC Press, 1997. — xxviii, 780 pages с. — ISBN 0849385237.
- Сингх, 2006, с. 97.
- Смарт, 2005, с. 84.
- Сингх, 2006, с. 32.
- Dr. C.-K. Shene. Kasiski's Method (2014).
- Bauer, Friedrich Ludwig, 1924-. Decrypted secrets : methods and maxims of cryptology. — Berlin: Springer, 1997. — xii, 447 pages с. — ISBN 9783540604181.
- Габидулин, 2011, с. 35.
- Смарт, 2005, с. 83.
Литература
- Габидулин Э. М., А. С. Кшевецкий, А. И. Колыбельников. Защита информации. — МФТИ, 2011. — 262 с.
- Н. Смарт. Криптография. — Техносфера, 2005. — 526 с.
- С. Сингх. Тайная история шифров и их расшифровки. — Астрель, 2006. — 447 с.
- Tilborg H.C.A. Fundamentals of Cryptography. A Professional Reference and Interactive Tutorial. — Kluwer, 1999. — 503 с.
- Menezes A.J., Oorschot P.C., Vanstone S.A. Handbook of Applied Cryptography. — CRC Press, 1996. — 816 с.
- Beutelspacher A. Cryptology
- Kahn D. The Codebreakers – The Story of Secret Writing - 1968
- Bishop M., Wesley A. Computer Security - 2003
