Медовое шифрование

В 1999 году Даглас Хувер и Нат Каузик рассмотрели проблему защиты закрытого ключа в криптосистемах с открытым ключом, в частности, секретной экспоненты в RSA и секретного ключа в DSA и предложили алгоритм маскировки этой секретной компоненты с помощью пароля (шести-восьмибитной строки). В своей работе они утверждали, что для таких паролей перебор по словарю будет давать результат такой же структуры, что и защищаемый закрытый ключ, и злоумышленник не сможет различить правильно расшифрованные данные от многих других правдоподобных, но ложных расшифровок, пока не попытается использовать полученные ключи для доступа к взламываемому ресурсу через сервер аутентификации. Сервер обнаружит несколько ошибок аутентификации и приостановит доступ. Такой подход обеспечивает дополнительную меру безопасности, что даёт возможность, например, уменьшить размерность пространства ключей[2].

В последующем были предложены системы[3][4] хранения паролей, использующие схожий метод маскировки сохраненных аутентификационных данных среди списка явно поддельных, для предотвращения рассекречивания базы данных в случае, к примеру, утечки хеш-файла паролей.

Основываясь на подобных системах маскировки, Ари Джулз из Корнеллского Университета и Томас Ристенпарт из Университета Висконсина представили доклад о медовом шифровании на конференции Eurocrypt 2014[5].

Медовое шифрование предназначено для защиты от атак, использующих метод полного перебора. Подобные атаки представляют собой взлом путём перебора всех возможных вариантов ключа, что эквивалентно выбору случайных открытых текстов из пространства всех возможных открытых текстов с дискретным равномерным распределением. Это может быть эффективным: несмотря на то что злоумышленник с равной вероятностью получает любой возможный открытый текст, большинство из них крайне неправдоподобны, другими словами, распределение разумных открытых текстов неравномерно. Механизм защиты медового метода основывается на преобразовании пространства открытых текстов в такое пространство, что распределение правдоподобных открытых текстов в нём равномерно. Таким образом, угадывающий ключи злоумышленник будет часто получать разумно выглядящие тексты, а случайно выглядящие тексты редко. Это затрудняет понимание, был ли угадан правильный ключ. В сущности, медовое шифрование выдаёт ложные данные в ответ на каждое неверное предположение о пароле или ключе шифрования[6].

Безопасность медового шифрования основана на том, что вероятность того, что злоумышленник сочтёт открытый текст верным, может быть рассчитана (шифрующей стороной) во время шифрования. Это затрудняет применение медового шифрования в определённых приложениях, где пространство открытых текстов очень велико или их распределение неизвестно. Также это означает, что медовое шифрование может быть уязвимо для атак методом «грубой силы», если эта вероятность будет неправильно посчитана. Например, он уязвим для атак на основе открытых текстов, если у злоумышленника есть «шпаргалка», это значит, что он обладает определённым числом открытых текстов и соответствующих им шифротекстов, это делает возможным перебор даже данных, зашифрованных медовым методом, если её наличие не было учтено при зашифровке[7].

К недостаткам алгоритма относится проблема опечаток: если доверенный пользователь ошибется при наборе ключа, то он получит поддельный открытый текст, выглядящий при этом правдоподобно, и у него не будет возможности понять это. Также актуален вопрос создания семантически и контекстно корректного ложного сообщения, которого будет достаточно, чтобы обмануть злоумышленника. Сгенерированные сообщения должны быть трудно отличимы от реальных сообщений, при этом они должны следовать правилам и нормам языка и в то же время скрывать значимую информацию из оригинального текста[8].

В медовом шифровании участвуют три набора: набор всех сообщений ${\displaystyle {\mathcal {M}}}$ (пространство сообщений), набор всех ключей ${\displaystyle {\mathcal {K}}}$ (пространство ключей) и набор так называемых промежуточных значений ${\displaystyle {\mathcal {S}}}$ (от англ. Seed). Также важной частью медового шифрования является кодер преобразования с распределением или DTE (от англ. Distribution Transforming Encoder), состоящий из двух алгоритмов кодирования и декодирования, устанавливающих связь между пространствами ${\displaystyle {\mathcal {M}}}$ и ${\displaystyle {\mathcal {S}}}$. При кодировании обычный текст сопоставляется с промежуточным значением с помощью DTE, а затем преобразуется в зашифрованный текст с использованием какого-либо симметричного метода шифрования c выбранным ключом. Процедура декодирования с ключом возвращает промежуточное значение, которое затем транслируется DTE в правильное сообщение[9].

Сообщение может быть сопоставлено нескольким промежуточным значениям, но каждое значение — только одному сообщению. Если для сообщения возможно несколько значений, в алгоритме кодирования случайно выбирается ровно одно. Таким образом, этот алгоритм кодирования рандомизирован, а алгоритм декодирования детерминирован. Количество значений, которые сопоставляются сообщению, должно быть пропорционально его вероятности. Таким образом, для создания DTE должно быть известно дискретное распределение вероятности появления сообщений[10].

При неправильном ключе зашифрованный текст сопоставляется с другим значением и, таким образом, расшифровывается в ложное сообщение[5].

• Зашифрованный номер кредитной карты подвержен атакам методом перебора, потому что не каждый набор цифр одинаково вероятен. Количество цифр может варьироваться от 13 до 19, хотя 16 является наиболее распространённым. Кроме того, он должен иметь действительный идентификационный номер IIN, а последняя цифра должна соответствовать контрольной сумме. Злоумышленник также может учитывать популярность различных сервисов: получить IIN из MasterCard, вероятнее, чем IIN из Diners Club Carte Blanche. Медовое шифрование может защитить от подобной атаки, сначала сопоставив номера кредитных карт областям в пространстве, где они соответствуют вероятности их легитимности. Номера с недействительными IIN и контрольными суммами вообще не отображаются на какую-либо область. Номера крупных брендов, таких как MasterCard и Visa, сопоставляются с большими подмножествами этого пространства, в то время как менее популярные сервисы отображаются с более мелкими подмножествами и так далее. Злоумышленник, перебирая такую схему шифрования, будет получать правдоподобные номера кредитных карт, и типы номеров будут появляться с ожидаемой им частотой[12].

Визуализация примера

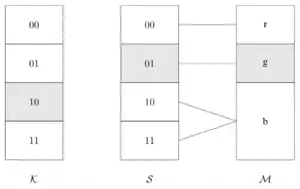
• Шифруется основной компонент из палитры RGB, поэтому все возможные сообщения — это r (красный), g (зелёный) и b (синий). Известно распределение вероятностей сообщений, а именно синий избирается с вероятностью 50 %, а два других сообщения — по 25 % каждое. DTE (справа на рисунке) сопоставляет выбранное сообщение с промежуточным значением (в центре). На рисунке сообщение, которое должно быть зашифровано зелёным цветом, присваивается значению 01. Ключ 10 теперь складывается по модулю 2 с этим значением:

${\displaystyle 01\oplus 10=11}$

11 — это шифротекст. Во время дешифрования зашифрованный текст повторно складывается по модулю 2 с ключом:

${\displaystyle 11\oplus 10=01}$

Это снова промежуточное значение, которое затем сопоставляется с исходным сообщением DTE. Сообщение снова расшифровано.

Если злоумышленник пробует ключ, например, 00, он складывает зашифрованный текст с этим ключом и получает ${\displaystyle 11\oplus 00=11}$, который декодируется синим цветом. Злоумышленник не может определить, является ли это сообщение правильным или неправильным[13].

Различные адаптации алгоритма медового шифрования находят свое применение в вопросе защиты данных, находящихся в облачных хранилищах, как пример реализация[14] дополнительной защиты для зашифрованных файлов, помимо пользовательского пароля. Если злоумышленник пытается получить доступ к зашифрованным данным с помощью перебора вариантов пароля методом «грубой силы», вместо того, чтобы запрещать доступ, алгоритм генерирует неразличимый поддельный файл, связанный с исходным файлом. Аналогичная система была предложена для защиты приложений, используемых в интернет-банкинге[15].

На конференции ICASSP 2016 был представлен концепт устойчивого к прослушиванию мессенджера, создающего правдоподобные сообщения при попытке атаковать зашифрованные сообщения[16].

• Juels A., Ristenpart T. Honey Encryption: Security Beyond the Brute-Force Bound // Advances in Cryptology – EUROCRYPT 2014. — Springer, 2014. — P. 293—310. — ISBN 978-3-642-55220-5. — ISSN 1611-3349. — doi:10.1007/978-3-642-55220-5_17.
• Juels A., Ristenpart T. Honey Encryption – Encryption beyond the Brute – Force Barrier // IEEE Security & Privacy, 12(4). — IEEE, 2014. — P. 59—62. — ISSN 1558-4046. — doi:10.1109/MSP.2014.67.
• Hoover D. N., Kausik B. N. Software smart cards via cryptographic camouflage // Proceedings of the 1999 IEEE Symposium on Security and Privacy. — IEEE, 1999. — P. 208—215. — ISBN 0-7695-0176-1. — ISSN 1081-6011. — doi:10.1109/SECPRI.1999.766915.
• Bojinov H., Bursztein E., Boyen X., Boneh D. Kamouflage: loss-resistant password management // Computer Security – ESORICS 2010. — Springer, 2010. — P. 286—302. — ISBN 3-642-15496-4. — ISSN 0302-9743. — doi:10.1007/978-3-642-15497-3_18.
• Juels A., Rivest R. Honeywords: Making password-cracking detectable // Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security. — ACM, 2013. — P. 145—160. — ISBN 978-1-4503-2477-9. — doi:10.1145/2508859.2516671.
• Omolara O. E., Jantan A., Abiodun O. I. A comprehensive review of honey encryption scheme // TELKOMNIKA Indonesian Journal of Electrical Engineering. — Universitas Ahmad Dahlan, 2019. — P. 649—656. — ISSN 2502-4752. — doi:10.11591/ijeecs.v13.i2.pp649-656.
• Yin W., Indulska J., Zhou H. Protecting Private Data by Honey Encryption // Security and Communication Networks Volume 2017. — Wiley, 2017. — P. 9. — ISSN 1939-0122. — doi:10.1155/2017/6760532.
• Mok E., Samsudin A., Tan S. F. Implementing the Honey Encryption for Securing Public Cloud Data Storage // First EAI International Conference on Computer Science and Engineering. — EAI, 2017. — P. 9. — doi:10.4108/eai.27-2-2017.152270.
• Samsudin A., Tan S. F. Enhanced Security of Internet Banking Authentication with EXtended Honey Encryption (XHE) Scheme // Innovative Computing, Optimization and Its Applications. — Springer, 2017. — P. 201—216. — ISBN 978-3-319-66984-7. — ISSN 1860-9503. — doi:10.1007/978-3-319-66984-7_12.
• Kim J. I., Yoon J. W. Honey chatting: A novel instant messaging system robust to eavesdropping over communication // 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). — IEEE, 2016. — P. 2184—2188. — ISBN 978-1-4799-9988-0. — doi:10.1109/ICASSP.2016.7472064.

• Веб-сайт конференции Eurocrypt 2014
• Mimoso, Michael. «Медовое» шифрование обманывает хакеров ложной дешифровкой (неопр.). threatpost (31 января 2014). Дата обращения: 20 декабря 2019.