Мартингал
Мартинга́л в теории случайных процессов — такой случайный процесс, что наилучшим (в смысле среднеквадратичного) предсказанием поведения процесса в будущем является его настоящее состояние.
- О системе в азартных играх см. Мартингейл; об элементе конской упряжи см. Мартингал
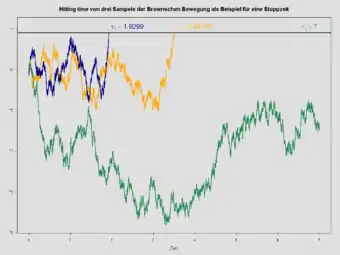
Остановленное броуновское движение как пример мартингала
Мартингалы с дискретным временем
- Последовательность случайных величин называется мартинга́лом с дискре́тным вре́менем, если
- ;
- .
- Пусть дана другая последовательность случайных величин . Тогда последовательность случайных величин называется мартингалом относительно или -мартингалом, если
- ;
- .
Мартингалы с непрерывным временем
Пусть есть вероятностное пространство с заданной на нём фильтрацией , где . Тогда случайный процесс называется мартингалом относительно , если
- измерима относительно для любого .
- .
- почти наверное, .[1]
Если в качестве взята естественная фильтрация , то называют просто мартингалом.
Суб- и супермартингалы
- Пусть дана последовательность случайных величин . Тогда последовательность случайных величин называется су́б(су́пер)мартингалом относительно , если
- Случайный процесс называется суб(супер)мартингалом относительно , если
- измерима относительно для любого .
- .
- .
Если в качестве взята естественная фильтрация , то называют просто суб(супер)мартингалом.
Свойства
- Случайный процесс является мартингалом тогда и только тогда, когда он является одновременно субмартингалом и супермартингалом.
- Если — мартингал, то .
- Если — субмартингал, то — супермартингал.
- Если является мартингалом, а — выпуклая функция, то — субмартингал. Если — вогнутая функция, то — супермартингал.
- Вообще говоря, мартингал не является марковским процессом.
- Верно и обратное: марковский процесс не обязан быть мартингалом.
Примеры
- Рассмотрим игру, при которой подбрасывается монета, и при выпадении «орла» игрок выигрывает 1 руб., а при выпадении «решки» проигрывает 1 руб. Тогда:
- если монета уравновешена, то состояние игрока как функция количества игр является мартингалом;
- если выпадение «орла» более вероятно, то состояние игрока — субмартингал;
- если выпадение «решки» более вероятно, то состояние игрока — супермартингал.
- Винеровский процесс (это математическая модель броуновского движения) является мартингалом.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.