Логарифмический декремент колебаний

Логарифми́ческий декреме́нт колеба́ний (декреме́нт затуха́ния; от лат. decrementum — «уменьшение, убыль») — безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины x в одну и ту же сторону:

${\displaystyle \lambda =\ln {\frac {x_{0}}{x_{1}}}.}$

Логарифм отношения амплитуд в точках, ограниченных периодом Т, равен логарифмическому декременту колебаний λ

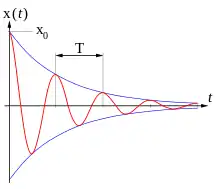
Логарифмический декремент колебаний равен коэффициенту затухания β, умноженному на период колебаний T:

${\displaystyle \lambda =\beta T.}$

Этот параметр применяется, как правило, для линейных колебательных систем, поскольку в нелинейных системах период колебания, вообще говоря, зависит от амплитуды, а закон убывания амплитуды отличается от экспоненциального. В линейных системах колеблющаяся величина изменяется со временем как

${\displaystyle x(t)=Ae^{-\beta t}\cos \omega t,}$

где A = x(0) — начальная амплитуда,

t — время,

ω = 2π/T — циклическая частота колебания.

Обозначив X_n = x(nT), получаем отсюда, что отношение величин X_k и X_k+1 равно

${\displaystyle X_{k}/X_{k+1}={\frac {e^{-\beta kT}}{e^{-(k+1)\beta T}}}\cdot {\frac {\cos(2\pi k)}{\cos(2\pi (k+1))}}=e^{\beta T}.}$

Логарифмический декремент равен показателю этой экспоненты:

${\displaystyle \lambda =\ln(X_{k}/X_{k+1})=\ln e^{\beta T}=\beta T.}$

Если энергия колебательной системы пропорциональна x, то её добротность (относительная потеря энергии за время нарастания фазы на 1 радиан) равна

${\displaystyle Q={\frac {2\pi }{1-e^{-\lambda }}},}$

а логарифмический декремент выражается через добротность как

${\displaystyle \lambda =-\ln \left(1-{\frac {2\pi }{Q}}\right).}$

Для систем с высокой добротностью (т. е. со слабым затуханием) ${\displaystyle \lambda \ll 1,}$ поэтому можно, разложив ${\displaystyle e^{-\lambda }}$ в ряд Маклорена по λ, ограничиться первыми двумя членами и заменить в этих формулах ${\displaystyle e^{-\lambda }}$ на ${\displaystyle 1-\lambda ,}$ что приводит к

${\displaystyle Q\approx {\frac {2\pi }{\lambda }},\qquad \lambda \approx {\frac {2\pi }{Q}}.}$