Линейное зондирование
Линейное зондирование — это схема в программировании для разрешения коллизий в хеш-таблицах, структурах данных для управления наборами пар ключ – значение и поиска значений, ассоциированных с данным ключом. Схему придумали в 1954 Джин Амдал, Элейн Макгроу и Артур Сэмюэл, а проанализировна она была в 1963 Дональдом Кнутом.
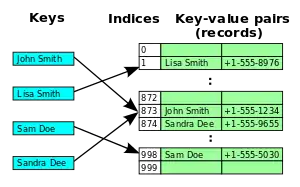
Вместе с квадратичным зондированием и двойным зондированием линейное зондирование является видом открытой адресации. В этих схемах каждая ячейка хеш-таблицы содержит одну пару ключ-значение. Если хеш-функция даёт коллизию, отображая значение нового ключа в ячейку хеш-таблицы, занятую другим ключом, линейное зондирование просматривает таблицу до ближайшей свободной следующей ячейки и вставляет новый ключ туда. Поиск значения осуществляется тем же образом, путём просмотра таблицы последовательно, начиная с позиции, определённой хеш-функцией, пока не найдёт совпадение ключа, либо пустую ячейку.
Как писали Торуп и Чжан, «Хеш-таблицы интенсивно используют нетривиальные структуры данных и большинство имплементаций в аппаратуре использует линейное зондирование, быстрое и простое в реализации»[1]. Линейное зондирование может дать высокую производительность вследствие хорошей локальности ссылок метода, но оно более чувствительно к качеству хеш-функции, чем другие схемы разрешения коллизий. Среднее ожидаемое время поиска у метода является константой, то же самое верно для вставки и удаления, если в имплементации используется случайный выбор хеш-функции, 5-независимое хеширование, или табличное хеширование. Однако, на практике, хорошие результаты получаются и с другими функциями хеширования, такими как MurmurHash [2].
Операции
Линейное зондирование является компонентом схем открытой адресации для использования в хеш-таблицах для решения словарных задач. В словарной задаче структура данных должна работать с набором пар ключ-значение и должна обеспечивать возможность вставки и удаления пар, а также поиск значения, ассоциированного с ключом. В открытой адресации структурой данных служит массив T (хеш-таблица), ячейки которого T[i] (если не пусты) содержат единственную пару ключ-значение. Хеш-функция используется для отображения каждого ключа в ячейку таблицы T, куда этот ключ должен быть занесён, как правило, скремблируя ключи, так что ключи с близкими значениями не оказываются близко в таблице. Коллизия хеш-функции возникает, когда хеш-функция отображает ключ в ячейку, уже занятую другим ключом. Линейное зондирование является стратегией для разрешения коллизий путём размещения нового ключа в ближайшую следующую свободную ячейки[3][4].
Поиск
Для поиска заданного ключа x проверяются ячейки таблицы T, начиная с ячейки с индексом h(x) (где h — хеш-функция), затем ячейки h(x) + 1, h(x) + 2, …, пока не будет найдена свободная ячейка или ячейка, в которой содержится ключ x. Если ячейка, содержащая ключ, найдена, процедура поиска возвращает значение из этой ячейки. В противном случае, если встретилась пустая ячейка, ключ не может находиться в таблице и процедура возвращает в качестве результата, что ключ не найден[3][4]
Вставка
Для вставки пары ключ-значение (x,v) в таблицу (возможно, с заменой любой существующей пары с тем же ключом) алгоритм вставки проходит ту же последовательность ячеек, что и при поиске, пока не найдёт либо пустую ячейку, либо ячейку, содержащую ключ x. Новая пара ключ-значение размещается в этой ячейке[3][4].
Если после вставки коэффициент загрузки таблицы (доля занятых ячеек) превышает некоторый порог, вся таблица может быть заменена на новую таблицу, размер которой увеличивается на постоянный множитель, как в случае динамического массива, с новой хеш-таблицей. Установка этого порога близким к нулю и использование высокого коэффициента расширения таблицы приводит к быстрым операциям, но требует больших затрат памяти. Обычно размер таблицы удваивается при достижении коэффициента загрузки 1/2, так что загрузка составляет от 1/4 до 1/2[5]
Удаление
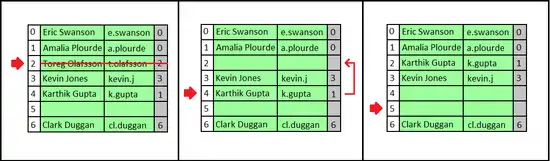
Можно удалить пару ключ-значение из словаря. Однако недостаточно просто очистить ячейку. Возможно, существует другая пара с тем же хеш-значением, которая была размещена где-то после занятой ячейки. После очистки ячейки поиск второго значения с тем же значением хеш-функции наткнётся на пустую ячейку, и пара не будет найдена.
Таким образом, при очистке ячейки i необходимо просмотреть последующие ячейки, пока не найдём пустую ячейку, либо ключ, который можно перенести в ячейку i (то есть ключ, хеш-значение которого равно или меньше i). Если найдена пустая ячейка, то можно очистить ячейку i и остановить процесс удаления. Если же найден ключ, который можно перенести в ячейку i, переносим его. Это приведёт к увеличению скорости поиска перенесённого ключа, а также очищает другую ячейку в блоке занятых ячеек. Необходимо продолжить поиск ключа, который может быть перенесён на это освободившееся место. Поиск ключа для переноса осуществляется до пустой ячейки, пока не достигнем ячейки, которая изначально была пуста. Таким образом, время выполнения всего процесса удаления пропорционально длине блока, содержащего удалённый ключ[3].
Альтернативно, можно использовать стратегию ленивого удаления, в которой пара ключ-значение удаляется путём замены значения специальным флагом, показывающим, что ключ удалён. Однако такие флаги приводят к увеличению коэффициента загрузки хеш-таблицы. В этой стратегии может стать необходимым удалить флаги из массива и пересчитать хеш-значения всех оставшихся пар ключ-значение, когда слишком много значений окажутся удалёнными[3][4].
Свойства
Линейное зондирование даёт хорошую локальность ссылок, что означает, что нужно лишь несколько некешированных операций доступа к память на одну операцию. Ввиду этого, при поддержке низкого коэффициента загрузки алгоритм может дать высокую степень производительности. Однако, по сравнению с некоторыми другими стратегиями открытой адресации, скорость работы деградирует быстрее при высокой степени загрузки ввиду первичной кластеризации, тенденции одной коллизии вызывать много близких коллизий [3]. Кроме того, для получения хорошей скорости работы этого метода требуется хеш-функция более высокого качества, чем для других схем разрешения коллизий[6]. Если алгоритм реализуется с хеш-функцией низкого качества, которая не исключает неоднородности во входном распределении, линейное зондирование может оказаться медленнее других стратегий открытой адресации, таких как двойное зондирование, которое пробует последовательность ячеек, разъединение которых определяется второй хеш-функцией, или квадратичное зондирование, когда размер каждого шага меняется в зависимости от позиции в последовательности проб[7].
Анализ
При использовании линейного зондирования операции со словарём могут быть имплементированы с постоянным ожидаемым временем доступа. Другими словами, операции вставки, удаления и поиска могут быть имплементированы за O(1), при условии, что коэффициент загрузки хеш-таблицы является константой, строго меньшей единицы[8].
Подробнее, время для каждой отдельной операции (поиск, вставка или удаление) пропорционально длине непрерывного блока занятых ячеек, с которого операция начинается. Если все начальные ячейки равновозможны в хеш-таблице с N ячейками, то максимальный блок k занятых ячеек имеет вероятность k/N содержать начальное положение поиска и займёт время O(k), где бы ни находилась стартовая ячейка. Таким образом, ожидаемое время выполнения операции можно вычислить как произведение этих двух членов, O(k2/N), суммированных по всем максимальным блокам непрерывных ячеек в таблице. Похожая сумма квадратов длин блоков дают границу мат. ожидания времени для случайной хеш-функции (а не случайное стартовое положение в хеш-таблице) путём суммирования по всем блокам, которые могут существовать (а не по тем, которые фактически существуют в текущем состоянии таблицы) и умножения членов для каждого потенциального блока на вероятность, что блок занят. То есть, если определить Block(i,k) как событие, что имеется максимальный непрерывный блок занятых ячеек длины k, начинающийся с индекса i, мат. ожидание времени на операцию равно
Формулу можно упростить путём замены Block(i,k) by a simpler necessary condition Full(k), the event that at least k elements have hash values that lie within a block of cells of length k. After this replacement, the value within the sum no longer depends on i, and the 1/N factor cancels the N terms of the outer summation. Эти упрощения приводят к границе
Но, согласно мультипликативной форме границы Чернова, если коэффициент загрузки строго меньше единицы, вероятность, что длина блока k содержит по меньшей мере k хешированных значений, является экспоненциально малой как функция от k, что означает, что сумма ограничена константой, не зависящей от n[3]. Можно также провести тот же анализ с помощью формулы Стирлинга вместо границы Чернова, чтобы оценить вероятность того, что блок содержит в точности k хешированных значений[4][9].
В терминах коэффициента загрузки α ожидаемое время успешного поиска равно O(1 + 1/(1 − α)), а ожидаемое время неуспешного поиска (или вставки нового ключа) равно O(1 + 1/(1 − α)2) [10]. Для постоянного коэффициента загрузки, с большой вероятностью, самая длинная последовательность зондирования (среди последовательностей зондирования для всех ключей из таблицы) имеет логарифмическую длину[11].
Выбор Хеш-функции
Поскольку линейное зондирование очень чувствительно для неравномерно распределённых значений хеш-функций[7], важно комбинировать метод с хеш-функцией высокого качества, которая не даёт такую неравномерность.
Анализ, приведённый выше, предполагает, что хеш каждого ключа является случайным числом, не зависящим от хешей других ключей. Это предположение нереалистично для большинства приложений с хешированием. Однако случайные или псевдослучайные хеш-значения могут быть использованы, когда объекты хешируются по их идентификатору, а не по значению. Например, так сделано с использованием линейного зондирования с помощью класса IdentityHashMap в наборе классов и интерфейсов Java collections framework[12]. Значение хеша, который этот класс ассоциирует с каждым объектом, его identityHashCode, гарантированно остаётся неизменным для объекта на протяжении его жизни, но хеш-значение для такого же объекта в других обстоятельствах будет другим[13]. Поскольку identityHashCode строится только раз для каждого объекта и не требуется его связь со значением или адресом объекта, его построение может использовать более медленные вычислительные средства, такие как вызов случайных или псевдослучайных генераторов чисел. Например, Java 8 для построения таких значений использует псевдослучайный числовой генератор Xorshift[14].
Для большинства приложений хеширования необходимо вычислять хеш-функцию для каждого значения каждый раз, когда требуется хеш, а не один раз, когда объект создаётся. В таких приложениях случайные или псевдослучайные числа не могут быть использованы в качестве хеш-значений, поскольку тогда различные объекты с тем же значением могли бы иметь различные значения хеша. А криптографические хеш-функции (которые создаются так, что они неотличимы от истинно случайных функций) обычно слишком медленны для использования в хеш-таблицах[15]. Вместо этого используются другие методы для построения хеш-функций. Эти методы вычисляют хеш-функцию быстро, и можно доказать, что они хорошо работают с линейным зондированием. В частности, линейное зондирование было проанализировано в рамках k-независимого хеширования, классе хеш-функций, которые инициализируются небольшим случайным числом с равной возможностью отображают любой k-кортеж различных ключей в любой k-кортеж индексов. Параметр k может рассматриваться как мера качества хеш-функции — чем больше k, тем больше времени нужно для вычисления хеш-функции, но она будет вести себя ближе к полностью случайным функциям. Для линейного зондирования 5-независимость достаточна, чтобы гарантировать постоянное ожидаемое время на операцию[16], в то время как некоторые 4-независимые хеш-функции работают плохо, требуя логарифмического времени на операцию[6].
Другой метод построения хеш-функций с высоким качеством и приемлемой скоростью — табличное хеширование. В этом методе значение хеша для ключа вычисляется путём выбора для каждого байта ключа индекса в таблице случайных чисел (с различными таблицами для каждой позиции байта). Числа из ячеек этих таблиц затем комбинируются побитно с помощью операции «исключающее ИЛИ». Хеш-функции, построенные таким образом, только 3-независимы. Тем не менее, линейные зондирования, использующие эти хеш-функции, требуют постоянного ожидаемого времени на операцию[4][17]. Как табличное хеширование, так и стандартные методы генерации 5-независимых хеш-функций лимитированы ключами, которые имеют фиксированное число бит. Для работы со строками или другими типами ключей переменной длины, можно скомбинировать более простую технику универсального хеширования, которая отображает ключи в промежуточные значения, с высокого качества (5-независимость или табуляция) хеш-функцией, которая отображает промежуточные значения в индексы хеш-таблицы[1][18].
В экспериментальных сравнениях Рихтер и др. нашли, что семейство хеш-функций с кратным сдвигом (определённых как ) было «наиболее быстрой хеш-функцией при использовании во всех схемах хеширования, то есть дающая самую высокую пропускную способность, а также хорошее качество», в то время как табличное хеширование давало «самую низкую пропускную способность»[2]. Они указали, что просмотр каждой таблицы требует несколько циклов, что более накладно, чем простые арифметические операции. Они также обнаружили, что MurmurHash лучше, чем табличное хеширование: «После изучения результатов, представленных Мультом и Мурмуром, мы думаем, что замена на табуляцию (…) на практике менее привлекательна».
История
Идея ассоциативного массива, которая позволяет получить доступ к данным по их значению, а не через их адрес, восходит к середине 1940-х годов к работам Конрада Цузе и Вэнивара Буша[19], но хеш-таблицы не были описаны, пока их не описал Лун в меморандуме IBM в 1953. Лун использовал другой метод разрешения коллизий, связь в цепочки, а не линейное зондирование[20].
Дональд Кнут[8] суммировал раннюю историю линейного зондирования. Это был первый метод открытой адресации и он был сначала синонимом открытой адресации. Согласно Кнуту, метод первым использовали Джин Амдал, МакГроу, Элани М. и Артур Сэмюэл в 1954 в ассемблерной программе для IBM 701[8]. Первое опубликованное описание линейного зондирования дал Петерсон[21][8], они же упомянули Сэмюэля, Амдала и МакГроу, но добавили, что «система столь естественна, что вполне вероятно, что могла быть независимо создана другими до или в то же время»[22]. Другая ранняя публикация этого метода принадлежит советскому исследователю Андрею Петровичу Ершову, вышедшая в 1958[23].
Первый теоретический анализ линейного зондирования, показывающий, что метод работает за постоянное ожидаемое время на операцию со случайной хеш-функцией, дал Кнут[8]. Седжвик назвал работу Кнута «вехой в анализе алгоритмов»[10]. Существенно позже исследования привели к более детальному анализу распределения вероятностей времени работы[24][25] и доказательство, что линейное зондирование работает за постоянное время на операцию с удобной для практических вычислений хеш-функцией, а не с идеальной случайной функцией, предполагаемой в ранних анализах[16][17].
Примечания
- Thorup, Zhang, 2012, с. 293–331.
- Richter, Alvarez, Dittrich, 2015, с. 293–331.
- Goodrich, Tamassia, 2015, с. 200–203.
- Morin, 2014, с. 108–116.
- Sedgewick, Wayne, 2011; Седжвик и Уэйн уменьшают вдвое размер таблицы, если при делении загрузка таблицы станет слишком низкой, что приводит к более широкому диапазону [1/8,1/2] возможных значений коэффициента загрузки.
- Pătraşcu, Thorup, 2010, с. 715–726.
- Heileman, Luo, 2005, с. 141–154.
- Knuth, 1963.
- Eppstein, 2011.
- Sedgewick, 2003.
- Pittel, 1987, с. 236–249.
- Java SE 7 Documentation.
- Friesen, 2012, с. 376.
- Kabutz, 2014.
- Weiss, 2014, с. 3—11.
- Pagh, Pagh, Ružić, 2009, с. 1107–1120.
- Pătrașcu, Thorup, 2011, с. 1–10.
- Thorup, 2009, с. 655–664.
- Parhami, 2006, с. 67.
- Morin, 2004, с. 9—15.
- Peterson, 1957.
- Peterson, 1957, с. 130–146.
- Ершов, 1958, с. 3–6.
- Flajolet, Poblete, Viola, 1998, с. 490–515.
- Knuth, 1998, с. 561–568.
Литература
- David Eppstein. Linear probing made easy. — 2011. — Октябрь.
- Donald Knuth. Notes on "Open" Addressing. — 1963.
- Gregory L. Heileman, Wenbin Luo. How caching affects hashing // Proceedings of the Seventh Workshop on Algorithm Engineering and Experiments and the Second Workshop on Analytic Algorithmics and Combinatorics. — Society for Industrial & Applied Mathematics,U.S., 2005. — С. 141–154. — ISBN 0898715962.
- Michael T. Goodrich, Roberto Tamassia. Section 6.3.3: Linear Probing // Algorithm Design and Applications. — Wiley, 2015. — С. 200–203. — ISBN 978-1-118-33591-8.
- Robert Sedgewick. Section 14.3: Linear Probing // Algorithms in Java, Parts 1–4: Fundamentals, Data Structures, Sorting, Searching. — Addison Wesley, 2003. — С. 615–620. — ISBN 9780321623973.
- Robert Sedgewick, Kevin Wayne. Алгоритмы. — 4th. — Addison-Wesley Professional, 2011. — ISBN 9780321573513.
- Pittel B. Linear probing: the probable largest search time grows logarithmically with the number of records // Journal of Algorithms. — 1987. — Т. 8, вып. 2. — С. 236–249. — doi:10.1016/0196-6774(87)90040-X.
- IdentityHashMap. Oracle. Дата обращения: 15 января 2016.
- Jeff Friesen. Beginning Java 7. — Apress, 2012. — С. 376. — (Expert's voice in Java). — ISBN 9781430239109.
- Heinz M. Kabutz. Identity Crisis // The Java Specialists' Newsletter. — 2014. — Сентябрь (т. 222).
- Mark Allen Weiss. Chapter 3: Data Structures // Computing Handbook. — 3rd. — CRC Press, 2014. — Т. 1. — С. 3—11. — ISBN 9781439898536.
- Pat Morin. Section 5.2: LinearHashTable: Linear Probing // Open Data Structures (in pseudocode). — 2014. — С. 108–116.
- Anna Pagh, Rasmus Pagh, Milan Ružić. Linear probing with constant independence // SIAM Journal on Computing. — 2009. — Т. 39, вып. 3. — С. 1107–1120. — doi:10.1137/070702278.
- Mihai Pătrașcu, Mikkel Thorup. On the k-independence required by linear probing and minwise independence // Automata, Languages and Programming, 37th International Colloquium, ICALP 2010, Bordeaux, France, July 6–10, 2010, Proceedings, Part I. — Springer, 2010. — Т. 6198. — С. 715–726. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-14165-2_60.
- Mihai Pătrașcu, Mikkel Thorup. The power of simple tabulation hashing // Proceedings of the 43rd annual ACM Symposium on Theory of Computing (STOC '11). — 2011. — С. 1–10. — doi:10.1145/1993636.1993638.
- Mikkel Thorup, Yin Zhang. Tabulation-based 5-independent hashing with applications to linear probing and second moment estimation // SIAM Journal on Computing. — 2012. — Т. 41, вып. 2. — С. 293–331. — doi:10.1137/100800774.
- Mikkel Thorup. String hashing for linear probing // Proceedings of the Twentieth Annual ACM-SIAM Symposium on Discrete Algorithms. — Philadelphia, PA: SIAM, 2009. — С. 655–664. — doi:10.1137/1.9781611973068.72.
- Stefan Richter, Victor Alvarez, Jens Dittrich. A seven-dimensional analysis of hashing methods and its implications on query processing // Proceedings of the VLDB Endowment. — 2015. — Т. 9, вып. 3. — С. 293–331.
- Behrooz Parhami. Introduction to Parallel Processing: Algorithms and Architectures. — Springer, 2006. — С. 67 4.1 Development of early models. — (Series in Computer Science). — ISBN 9780306469640.
- Pat Morin. Hash tables // Handbook of Data Structures and Applications / Dinesh P. Mehta, Sartaj Sahni. — Chapman & Hall / CRC, 2004. — С. 9—15. — ISBN 9781420035179.
- Peterson W. W. Addressing for random-access storage // IBM Journal of Research and Development. — Riverton, NJ, USA: IBM Corp., 1957. — Апрель (т. 1, вып. 2). — С. 130–146. — doi:10.1147/rd.12.0130.. Другая ранняя публикация этого метода принадлежит советскому исследователю Ершову А. П., in 1958.
- А. П. Ершов. {{{заглавие}}} // Доклады АН УССР. — 1958. — Вып. 118 (3). — С. 427–430.. Линейное зондирование описано как алгоритм A2.
- Flajolet P., Poblete P., Viola A. On the analysis of linear probing hashing // Algorithmica. — 1998. — Т. 22, вып. 4. — С. 490–515. — doi:10.1007/PL00009236.
- Donald Knuth. Linear probing and graphs // Algorithmica. — 1998. — Т. 22, вып. 4. — С. 561–568. — doi:10.1007/PL00009240.