Задача Бюффона о бросании иглы

Суть метода была в бросании иглы длиной ${\displaystyle L}$ на плоскость, расчерченную параллельными прямыми, расположенными на расстоянии ${\displaystyle r}$ друг от друга (см. Рис. 1).

Рисунок 1. Метод Бюффона

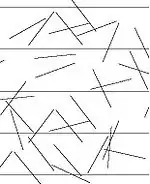
Вероятность (как видно из дальнейшего контекста, речь идёт не о вероятности, а о математическом ожидании количества пересечений за один опыт; вероятностью это становится лишь при условии, что ${\displaystyle r>L}$) того, что отрезок пересечет прямую, связана с числом Пи:

${\displaystyle p=\int \limits _{0}^{\pi }\int \limits _{0}^{l\sin {\theta }}{\frac {1}{r\pi }}dAd\theta }$, где

• ${\displaystyle A}$ — расстояние от начала иглы до ближайшей к ней прямой;
• ${\displaystyle \theta }$ — угол иглы относительно прямых.

При условии, что ${\displaystyle r>L}$ получается решение: ${\displaystyle p={\frac {2L}{r\pi \,}}}$. Таким образом, подсчитав долю отрезков, пересекающих прямые, можно приближенно определить число Пи. При увеличении количества попыток точность получаемого результата будет увеличиваться.

В 1864 году капитан Фокс, выздоравливая после ранения, чтобы как-то занять себя, реализовал эксперимент по бросанию иглы[1]. Результаты представлены в следующей таблице:[2]

Комментарии:

• Вращение плоскости применялось[2] (и как показывают результаты — успешно) для того, чтобы уменьшить систематическую ошибку.
• В третьей попытке длина иглы была больше расстояния между линиями, что позволило не увеличивая числа бросаний эффективно увеличить число событий и повысить точность.

• Задача о макаронине Бюффона — вариант задачи для кривых.[3]

• Формула Крофтона

• Федотов Н. Г. Методы стохастической геометрии в распознавании образов. — М.: Радио и связь, 1990. — 142 с.