Дуговая эластичность
Дуговая эластичность (англ. Arc elasticity) – показатель процентного изменения спроса или предложения на изменения цены, дохода или других факторов. Показатель используется при существенном изменении цены, дохода или других факторов, а в противном случае используется показатель точечной эластичности.
История создания
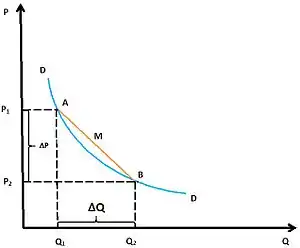
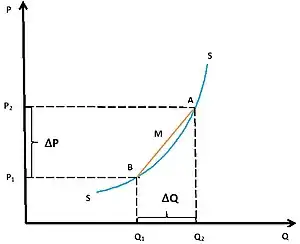
В случае анализа эластичности спроса или предложения с показателем точечной эластичности возникает проблема, что при выборе двух различных точек и как показано на рисунках «Дуговая эластичность спроса» и «Дуговая эластичность предложения» для базового расчёта процентных изменений, результат вычислений будет отличен между собой. Для преодоления этой проблемы используется в качестве исходной базы вычислений средние значения, рассчитанные по первоначальным и конечным ценам и количеству проданных или произведенных товаров или услуг. Такое решение позволяет оценить эластичность в центральной точке анализируемого отрезка на кривой линии спроса или на кривой линии предложения [1].
Определение
Дуговая эластичность спроса – степень реакции спроса на изменения цены, дохода и других факторов. Показатель эластичности спроса , определяющий эластичность в середине отрезка, соединяющие две точки, рассчитывается как[2]:
- ,
где - это спрос, - исходное количество проданного товара, - новый объём спроса, - исходная цена товара, - новая цена товара, , - изменение спроса и цены.
Дуговая эластичность предложения – степень реакции функции предложения на изменения цены или других факторов. Показатель эластичности предложения , определяется также:
- ,
где - это предложение, - исходное количество произведенного товара, - новый объём предложения, - исходная цена товара, - новая цена товара, , - изменение предложения и цены.
Значения
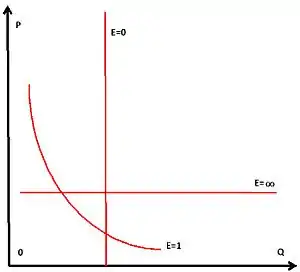
Когда коэффициент дуговой эластичности спроса равен бесконечности , то спрос совершенно эластичен. Незначительное увеличение цены приводит к бесконечно большому сокращению спроса, а малое снижение цены приводит к бесконечно большому увеличению объёма спроса. Кривая спроса имеет горизонтальную прямую[2].
Когда коэффициент дуговой эластичности спроса равен единице , то спрос имеет единичную эластичность, то есть изменение цены на 1% приводит к изменению объёма спроса на 1%. Кривая спроса имеет форму равнобочной гиперболы[2].
Когда коэффициент дуговой эластичности спроса нулевой , то спрос совершенно неэластичен, а любые изменения цены не влияют на объём спроса. Кривая спроса имеет вертикальную прямую[2].
Когда коэффициент дуговой эластичности спроса находится в интервале от ноля до единицы , то спрос неэластичен, то есть увеличение (снижение) цены на 1% приводит к снижению (повышению) объёма спроса менее чем на 1%[2].
Когда коэффициент дуговой эластичности спроса находится в интервале от единицы до бесконечности , то спрос эластичен, то есть увеличение (снижение) цены на 1% приводит к снижению (повышению) объёма спроса более чем на 1%[2].
Использование
Дуговая эластичность используется в случаях существенных изменений цен, доходов и других факторов. А сам показатель дуговой эластичности определяется между двумя показателями точечной эластичности для низкой и высокой цены, и не всегда определяется посередине[3].
Формула дуговой эластичности даёт приемлемую точность при аппроксимации точечной эластичности, если изменения цены и/или количества несущественны. По данным Вечканова Г. С. под существенным изменениями, как правило, понимается изменения свыше 5% от начальных величин[4], что приводит к существенному продвижению вдоль кривой спроса или предложения[5].
Показатель дуговой эластичности используется также, когда функция спроса или предложения не определена.
См. также
Примечания
- Макконнелл К.Р., Брю С.Л. Экономикс: Принципы, проблемы и политика. В 2 т.. — М.: Республика, 1992. — Т. 2. — С. 16. — 400 с. — ISBN 5-250-01486-0.
- Гальперин В. М., Игнатьев С. М., Моргунов В. И. Микроэкономика. В 3 томах. — СПб.: Омега-Л, Экономикус, 2010. — Т. 1. — 1026 с. — ISBN 978-5-370-01549-6.
- Пиндайк Р., Рубинфельд Д. Микроэкономика. — М.: Экономика, Дело, 1992. — С. 118. — 510 с. — ISBN 5-282-01225-1.
- Вечканов Г. С., Вечканова Г. Р. Микроэкономика: Учебник для вузов. — СПб.: Издательский дом «Питер», 2012. — С. 130. — 464 с. — ISBN 978-5-459-00407-6.
- Хайман Д. Н. Современная микроэкономика: анализ и применение. В 2-х т.. — М.: Финансы и статистика, 1992. — Т. 1. — С. 158. — 384 с. — ISBN 5-279-01135-5.