Динострат
Динострат (др.-греч. Δεινόστρατος, лат. Dinostratus, ок. 390 до н. э. — ок. 320 до н. э.) — древнегреческий математик, член Платоновской Академии, ученик Евдокса, брат математика Менехма.
| Динострат | |
|---|---|
| Δεινόστρατος | |
| Дата рождения | около 390 года до н. э. |
| Место рождения | |
| Дата смерти | около 320 года до н. э. |
| Место смерти | |
| Научная сфера | геометрия |
| Известен как | исследователь конических сечений и квадратрисы |
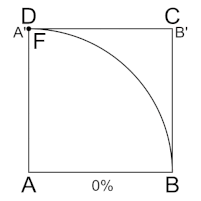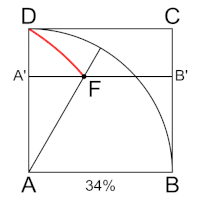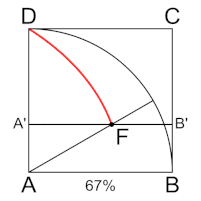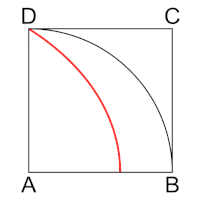
Папп в IV книге Математического собрания сообщает, что Динострат решил задачу о квадратуре круга с помощью квадратрисы. (Эту механическую кривую изобрёл Гиппий Элидский, решивший с её помощью задачу о трисекции угла). Динострат доказывает, что отрезок, отсекаемый квадратрисой на нижней стороне квадрата (см. рис.), так относится к стороне квадрата, как радиус окружности относится к длине дуги, составляющей четверть этой окружности.
Динострат упоминается также у Прокла Диадоха, который пишет, что они с Менехмом «сделали геометрию более совершенной». Есть основания полагать, что Динострат, как и его брат Менехм, занимался коническими сечениями. Он впервые сформулировал (на геометрическом языке) первый замечательный предел.
Литература
- Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — 456 с.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Прасолов В. В. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. — М.: Наука, 1992. — 80 с. — (Популярные лекции по математике).
- Щетников А. И. Как были найдены некоторые решения трёх классических задач древности? // Математическое образование. — 2008. — № 4 (48). — С. 3—15.
- Knorr W. R. The ancient tradition of geometric problems. Boston: Birkhäuser, 1993.
Ссылки
- O’Connor, John J; Edmund F. Robertson. Dinostratus. (англ.)