Геодезическая система координат

Геодези́ческая систе́ма координа́т — система координат, используемая для определения местоположения объектов на Земле. Отсчётной поверхностью является эллипсоид вращения или Ортогональная система координат, представляющий собой референц-версию, то есть адаптированный к какой-либо территории датум, геоцентрической системы координат.

Геодезические координаты используются в геодезии и навигации, в топографической съемке и картографии, а также спутниковыми навигационными системами для определения местоположения объектов на Земле в реальном времени. Положение точки в геодезической системе координат характеризуется математическими координатами абсциссой — $Y,$ ординатой — $X$ и аппликатой — $Z,$ и астрономическими:широтой — $B,$ долготой — $L$ и зенитом — $H.$ Которые, в свою очередь, взаимосвязаны между собой через геодезический азимут.

Геодезическая прямоугольная система координат (Математическая локальная)

Рисунок 1. Проекция приведенной широты на ось абсцисс.

В геодезии используют прямоугольную систему координат, начало $O$ которой находится в центре масс Земли, ось $Z$ направлена по оси вращения Земли, ось $X$ совмещена с линией пересечения плоскостей экватора и начального (гринвичского) меридиана, ось $Y$ дополняет систему до правой. Такую систему координат называют геоцентрической или общеземной. В общеземной системе координат определяют положение пунктов на всей поверхности Земли. К таким можно отнести WGS-84, GRS80, ПЗ-90.

Если система координат введена для определения положения точек на части земной поверхности, например, на территории одного государства, её начало $O$ может быть значительно (до сотен метров) смещено относительно центра масс. В этом случае говорят о референцной системе координат.

Из-за неизбежных ошибок измерений при практическом задании общеземной системы возможно несовпадение её начала с центром масс Земли и повороты осей. В связи с этим существуют несколько реализаций общеземной геоцентрической системы координат, и возникает необходимость перехода от одной системы координат к другой. Задача преобразования координат возникает также при переходе от референцной системы координат к общеземной и обратно[1].

Переход от одной прямоугольной системы координат к другой при одновременном переносе начала системы и повороте осей выполняют с помощью преобразования Гельмерта. Преобразование Гельмерта это преобразование с 7 элементами, с 3 параметрами смещения $c_{x},~c_{y},~c_{z},$ 3 параметрами разворота $r_{x},~r_{y},~r_{z}$ и 1 масштабным параметром $s.$ Преобразование Гельмерта — это приближённый метод, который можно считать точным только, когда параметры преобразования малы по сравнению с величинами векторов геоцентрической системы координат или такие параметры не учитываются. С такими условиями преобразование можно считать обратимым. Прочие последующие преобразование (преобразование Молоденского — 10 параметров и преобразование Молоденского — Бадекаса — 14 параметров), учитывающие дополнительные данные, осуществляются в несколько этапов, сложны и, как правило, необратимы. ввиду чего такие системы координат создаются строго на локальных участках с помощью Геодезических сетей III, IV классов, 1 и 2 разрядов. И используемые для решения исключительно прикладных задач на территории по площади не превышающей 3000—5000 км²[2][3][4][5].

Геодезическая эллипсоидальная система координат (Астрономическая глобальная)

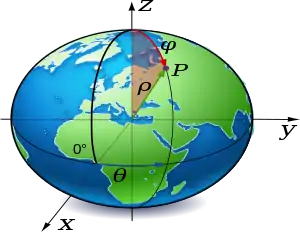
Рисунок 2. Геодезическая эллипсоидальная система координат.

Геодезическая эллипсоидальная система координат $B,~L,~H$ связана с эллипсоидом. Координатными линиями в этой системе являются нормали к эллипсоиду.

Геодезическая широта $B$ — это угол между нормалью $PP_{o}~O_{p}$ к эллипсоиду и плоскостью экватора.

Геодезическая долгота $L$ — угол между плоскостью $Y=0$ начального меридиана и плоскостью $ZOP$ меридиана точки $P.$

Геодезическая высота $H$ — отрезок $P_{o}~P$ нормали к эллипсоиду^[как?].

Формулы перехода

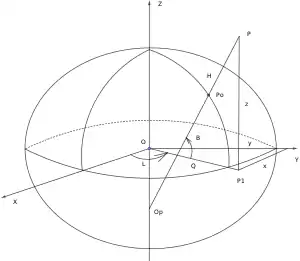
Рисунок 3. Связь геодезических прямоугольной и эллипсоидальной систем координат.

Геодезические прямоугольные и эллипсоидальные системы согласованы друг с другом. Центры этих систем совмещены, ось $Z$ прямоугольной системы проходит вдоль малой оси эллипсоида, оси $X$ и $Y$ совпадают. Связь систем устанавливают формулы представленные ниже.

Прямой переход

X=(N+H)\cos B\cos L;

Y=(N+H)\cos B\sin L;

Z=(N+H-Ne^{2})\sin B,

где

N

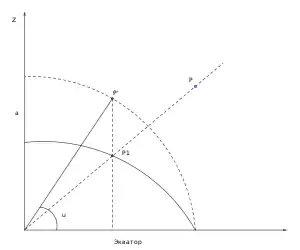
— радиус кривизны первого вертикала, равный отрезку

O_{p}~P_{o}

на рисунке 3,

e

— эксцентриситет.

$N$ находится по формуле:

N=a/\surd (1-e^{2}\sin ^{2}B),

где

a

— большая полуось эллипсоида[1].

Обратный переход

От геодезических эллипсоидальных координат к прямоугольным выполняют следующим образом: определяют долготу $L$ и радиус $Q$ параллели точки $P$ — отрезок $OP1.$ Это возможно сделать разными способами, например:

tgL=Y/X;Q=X\cos L+Y\sin L,

или:

Q={\sqrt {(}}X^{2}+Y^{2});\sin L=Y/Q;\cos L=X/Q.

Для широты находят:

tgB=(Z+Ne^{2}\sin B)/Q.

Широту $B$ вычисляют методом приближений, причем в начальном приближении можно использовать разные её значения. Наиболее удобно найти в первом приближении приведенную широту $u$ точки $P1$ отсчетного эллипсоида, лежащего на пересечении его поверхности с радиусом-вектором внешней точки $P$ [1]:

\operatorname {tg} u=Z/(Q{\sqrt {(}}1-e^{2})/

Приведенной широтой точки $P1$ эллипсоида называют геоцентрическую широту точки $P',$ являющейся проекцией точки $P1$ на вспомогательную сферу радиуса а нормалью к плоскости экватора. Приведенная и геодезическая широта связаны равенством:

\operatorname {tg} u={\sqrt {(}}1-e^{2})\operatorname {tg} B.

После вычисления приведенной широты геодезическую широту находят по формуле Боуринга:

\operatorname {tg} B=(Z+e^{2}(a\sin ^{3}a)/({\sqrt {(}}1-e^{2})\operatorname {tg} B))/(Q-e^{2}a\cos ^{3}a)

Геодезическую высоту $H$ вычисляют по формуле:

$H=Q\cos B+Z\sin B-a{\sqrt {(}}1-e^{2}\sin ^{2}B)$ [1].

Референцные (Аппроксимированные приближенные)

Отсчетный эллипсоид может располагаться внутри Земли по-разному. Если центр эллипсоида совмещен с центром масс Земли, а его поверхность близка к поверхности геоида, то эллипсоид называют геоцентрическим, не стоит путать с общеземным. Если эллипсоид близок к геоиду на ограниченной площади, а центр его смещен относительно центра масс, его называют референц-эллипсоидом. Референц-эллипсоид, как правило, устанавливается для использования в геодезический работах в той или иной стране, отсюда и его название (референция, то есть рекомендация)[1].

Данная система, основанная на Референц-эллипсоиде, поддерживалась и использовалась в ряде научных и прикладных задач до 1961 пунктами Лапласа и астропунктами II класса, которые были частично обращены в Геодезические сети сгущения II класса, и продолжались использоваться как экспедиционные пункты II класса преимущественно в необжитых и мало обжитых районах, как обоснования для мелкомасштабных географических съемок. После 1961 г геодезические сети II класса начинают строить в виде сплошных сетей треугольников, полностью заполняющих полигоны АГС I. Работы по созданию государственной геодезической сети были в основном закончены к 1989 году. Сеть пунктов I-го и II-го классов сплошь покрывала территорию страны. В 1990 году приказом ГУГК при Совете Министров СССР создано опытно-производственное подразделение МАГП (Московского аэрогеодезического предприятия) для производства работ с использованием спутниковых систем в соответствии с концепцией перехода топографо-геодезического производства на современные методы спутниковых определений, получившее наименование ВАГП (Верхневолжского аэрогеодезического предприятия). Результаты работ проводимых в 1991 показали не удовлетворительное состояние сети. В 1993—1995 в уравнивание включены: Космическая и Доплеровская сети (служившие основанием для Геоцентрической системы ПЗ-90). В 1996 было проведено заключительного уравнивания и к концу 1990-х, построена сеть из 134 опорных пунктов ГГС включавших 35 пунктов КГС и ДГС, покрывающая всю территорию страны при среднем расстоянии между смежными пунктами 400—500 км[6][7][8][9][10][11].

Постановлением правительства РФ от 24 ноября 2016 года за номером 1240 использование системы координат СК-42 допускается до 1 января 2021 г. Взамен вводится геоцентрическая система ГСК-2011 основанная на ПЗ-90 (являющаяся датумом общеземного элипсоида ITRF).

Земной эллипсоид

Эллипсоид можно задать двумя параметрами:

Параметр	Символ
Большая полуось	а
Геометрическое сжатие	$1/f$

Из а и $1/f$ можно вывести другие параметры эллипсоида:

Параметр	Символ
Малая полуось	$b=a(1-f)$
Первый эксцентриситет	$e^{2}=1-b^{2}/a^{2}=f(2-f)$
Второй эксцентриситет	$e'^{2}=a^{2}/b^{2}-1=(f(2-f))/(1-f)^{2}$

Список литературы

Огородова Л. В. Высшая геодезия. Часть III. Теоретическая геодезия, Москва, Геодезкартиздат 2006. ISBN 5-86066-076-6[1]
Сайт Информационно-аналитического центра координатно-временного и навигационного обеспечения. Прикладной потребительский центр ГЛОНАСС.

Ссылки

https://geographiclib.sourceforge.io (включает в себя утилита CartConvert, который преобразует геодезические координаты в геоцентрические (ECEF) или в локальные декартовые (ENU) координаты. Это обеспечивает точные результаты для всех входных данных, включая точки, близкие к центру Земли.
https://www.mathworks.com/matlabcentral/fileexchange/15285-geodetic-toolbox (Набор геодезических функций, которые решают различные задачи геодезии в среде Matlab).

См. также

Примечания

Огородова Л. В. Высшая геодезия. Часть III. Теоретическая геодезия / рецензенты=В. Н. Баранов рецензенты=А. Н. Зуева. — Москва: Геодезкартиздат, 2006. — С. 36–41. — 384 с. — ISBN 5-86066-076-6.
Geomatics Guidance Note Number 7, part 2. Coordinate Conversions and Transformations including Formulas (неопр.) (недоступная ссылка). International Association of Oil and Gas Producers (OGP). Архивировано 6 марта 2014 года.
Судаков С. Г. § 2. Схема построения геодезической сети СССР // Основные Геодезические Сети. — Москва: "Недра", 1975. — С. 24—25. — 368 с.
Яковлев Н. В. § 10. Геодезические сети. Их назначение. // Высшая геодезия. — Москва: Недра, 1989. — С. 35. — 445 с. — 8600 экз.
Генике А. А., Побединский Г. Г. § 7.4. Создание и реконструкция городских геодезических сетей с использованием спутниковых технологий. // Глобальные спутниковые системы определения местоположения и их применение в геодезии.. — Москва: ФГУП «Картгеоцентр», 2004. — С. 249. — 352 с.
Судаков С. Г. 1. Развитие Основных геодезических сетей в СССР // Основные Геодезические Сети. — Москва: "Недра", 1975. — С. 9,21. — 368 с.
Яковлев Н. В. § 18. Построение Государственной геодезической сети СССР в соответствии с основными положениями 1954—1961 гг. // Высшая геодезия. — Москва: Недра, 1989. — С. 63. — 445 с. — 8600 экз.
Пандул И. С. 6.1. Задачи геодезической астрономии. Классификация астропунктов // Геодезическая Астрономия Применительно к решению инженерно-геодезических задач. — Санкт-Петербург: "Политехника", 2010. — С. 162—163. — 324 с.
Генике А. А. Побединский Г. Г. 7.3. Построение государственной геодезической сети России на основе спутниковых технологий // Глобальные спутниковые системы определения местоположения и их применение в геодезии. — Москва: ФГУП «Картгеоцентр», 2004. — С. 246,269. — 352 с.
Ермаков В. С., Михаленко Е. Б., Загрядская Н. Н., Беляев Н. Д., Духовской Ф. Н. 2. ГОСУДАРСТВЕННЫЕ ГЕОДЕЗИЧЕСКИЕ СЕТИ // Инженерная геодезия. Геодезические сети. — Санкт-Петербург: Санкт-Петербургский государственный политехнический университет, 2003. — С. 11,16. — 40 с.
Антонович К. М. 2 Системы координат и времени в спутниковых технологиях // Использование спутниковых радионавигационных систем в геодезии. — Москва, 2006. — Т. 1. — С. 66,67.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] Огородова Л. В. Высшая геодезия. Часть III. Теоретическая геодезия / рецензенты=В. Н. Баранов рецензенты=А. Н. Зуева. — Москва: Геодезкартиздат, 2006. — С. 36–41. — 384 с. — ISBN 5-86066-076-6.

[2] Geomatics Guidance Note Number 7, part 2. Coordinate Conversions and Transformations including Formulas (неопр.) (недоступная ссылка). International Association of Oil and Gas Producers (OGP). Архивировано 6 марта 2014 года.

[3] Судаков С. Г. § 2. Схема построения геодезической сети СССР // Основные Геодезические Сети. — Москва: "Недра", 1975. — С. 24—25. — 368 с.

[4] Яковлев Н. В. § 10. Геодезические сети. Их назначение. // Высшая геодезия. — Москва: Недра, 1989. — С. 35. — 445 с. — 8600 экз.

[5] Генике А. А., Побединский Г. Г. § 7.4. Создание и реконструкция городских геодезических сетей с использованием спутниковых технологий. // Глобальные спутниковые системы определения местоположения и их применение в геодезии.. — Москва: ФГУП «Картгеоцентр», 2004. — С. 249. — 352 с.

[6] Судаков С. Г. 1. Развитие Основных геодезических сетей в СССР // Основные Геодезические Сети. — Москва: "Недра", 1975. — С. 9,21. — 368 с.

[7] Яковлев Н. В. § 18. Построение Государственной геодезической сети СССР в соответствии с основными положениями 1954—1961 гг. // Высшая геодезия. — Москва: Недра, 1989. — С. 63. — 445 с. — 8600 экз.

[8] Пандул И. С. 6.1. Задачи геодезической астрономии. Классификация астропунктов // Геодезическая Астрономия Применительно к решению инженерно-геодезических задач. — Санкт-Петербург: "Политехника", 2010. — С. 162—163. — 324 с.

[9] Генике А. А. Побединский Г. Г. 7.3. Построение государственной геодезической сети России на основе спутниковых технологий // Глобальные спутниковые системы определения местоположения и их применение в геодезии. — Москва: ФГУП «Картгеоцентр», 2004. — С. 246,269. — 352 с.

[10] Ермаков В. С., Михаленко Е. Б., Загрядская Н. Н., Беляев Н. Д., Духовской Ф. Н. 2. ГОСУДАРСТВЕННЫЕ ГЕОДЕЗИЧЕСКИЕ СЕТИ // Инженерная геодезия. Геодезические сети. — Санкт-Петербург: Санкт-Петербургский государственный политехнический университет, 2003. — С. 11,16. — 40 с.

[11] Антонович К. М. 2 Системы координат и времени в спутниковых технологиях // Использование спутниковых радионавигационных систем в геодезии. — Москва, 2006. — Т. 1. — С. 66,67.