Гармоническая четвёрка

Гармоническая четвёрка точек — чётверка точек на проективной прямой, двойное отношение которых $(ABCD)=-1$ . В этом случае говорят также, что точки $C$ и $D$ гармонически сопряжены относительно $A,B$ и пишут $H(AB,CD)$ .

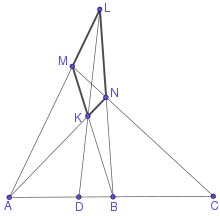
A, B, C, D — гармоническая четвёрка точек.

Гармонической четвёркой прямых называется четвёрка прямых $a,b,c,d$ в проективной плоскости, проходящих через одну точку $S$ , для которых любая четвёрка точек $A,B,C,D$ , такая, что $A\in a,B\in b,C\in c,D\in d$ , находящаяся на одной прямой, является гармонической. В этом случае пишут $H(ab,cd)$ .

Свойства

Если гармоническая четвёрка прямых пересечена прямой, то на этой прямой образуется гармоническая четвёрка точек.
На каждой стороне полного четырёхвершинника имеется гармоническая четвёрка точек.^{[уточнить]}
На каждой диагонали полного четырёхвершинника имеется гармоническая четвёрка точек.^{[уточнить]}
Гармоническая четвёрка точек на комплексной плоскости лежит на одной прямой или окружности, и пары касательных в противоположных точках конкурентны диагонали.

Построение

Для любых трёх точек, лежащих на одной прямой, пользуясь гармоническими свойствами полного четырёхвершинника, можно построить четвёртую точку так, что получится гармоническая четвёрка точек.
На рисунке выше точки пересечения двух пар противоположных сторон ML и KN, MK и LN полного четырёхугольника MLNK (соответственно первые две точки A и B прямой), а также точки D и C пересечения соответственно диагоналей LK и MN с этой прямой (прямая AC), проходящей через эти точки, образуют гармоническую четвёрку точек A, B, C, D.
Построения последнего пункта (см. также рисунок) полностью дублирует следующая теорема[1]: Для точки K прямая Чевы (например LD) треугольника ALB и прямая MN, соединяющая основания M и N двух других прямых Чевы AN и BM, делят противоположную сторону AB гармонически.

Пример гармонической четвёрки точек

Биссектрисы внутреннего и внешнего углов при одной вершине треугольника пересекают противоположную этой вершине сторону и соответственно её продолжение в двух точках, которые вместе с двумя концами этой стороны образуют гармоническую четвёрку точек[2].
Точка, гармонически сопряженная середине стороны треугольника, находится на продолжении этой стороны на бесконечности[3].

Гармоническая четвёрка на расширенной евклидовой плоскости

Если точка $D_{\infty }$ несобственная, то четвёрка $A,B,C,D_{\infty }$ гармоническая, если $C$ — середина отрезка $AB$ .
Если $ABCD$ — полный четырёхвершинник и его диагональные точки $P_{\infty },Q_{\infty }$ — несобственные, то на расширенной евклидовой плоскости $ABCD$ — параллелограмм, а из его гармонических свойств следует, что точка пересечения его диагоналей делит их пополам.
Если $ABCD$ — полный четырёхвершинник, у которого одна диагональная точка $R_{\infty }=BC\cap AD$ — несобственная, $P=AB\cap CD,Q=AC\cap BD$ , то на расширенной евклидовой плоскости $ABCD$ — трапеция, а из его гармонических свойств следует, что $PQ$ делит $AD$ пополам.

Примечания

Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. Теорема на с. 46, § 31.
Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. Теорема на с. 46, § 30.
Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. Задача на с. 46, § 30.

Литература

Базылев, Дуничев, Иваницкая. Геометрия, часть 2. — М.: Просвещение, 1975.

Ефимов Н. В. Высшая геометрия. — 6-е изд.. — М., 1978.

Певзнер С.Л. Проективная геометрия. — М.: Просвещение, 1980.

Постников М. М. Аналитическая геометрия. — 1973.

Х. С. М. Кокстер. Действительная проективная плоскость / под ред. проф. А. А. Глаголева. — М., 1959.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. Теорема на с. 46, § 31.

[2] Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. Теорема на с. 46, § 30.

[3] Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. Задача на с. 46, § 30.