Выбор материала
Выбор материала — это один из этапов в процессе проектирования конструкции[1]. При разработке изделия, часто основной целью выбора материала является минимизация затрат при достижении установленных требований к детали, например, высокой жесткости, малой массы и так далее, в зависимости от назначения изделия[1]. Так, детали теплообменного аппарата, которые разделяют среды, должны иметь высокую теплопроводность, чтобы максимизировать теплопередачу, и низкую себестоимость, чтобы теплообменный аппарат был конкурентоспособным[2].
Очень важно, чтобы разработчик конструкции обладал глубокими знаниями свойств материалов и их поведения при эксплуатации. Некоторые из важных критериев для выбора материалов: прочность, жесткость, плотность, теплостойкость, устойчивость к коррозии, обрабатываемость, свариваемость, закаливаемость, электропроводность и т. д.[3]
Методология выбора материала для изделий, требующих нескольких критериев, является более сложной, чем для одного критерия. Например, для изделия, которое должно быть жестким и легким, требуется материал с высоким модулем упругости и низкой плотностью. Если речь идет о стержне подверженном растяжению, то чтобы определить оптимальный критерий для выбора материала необходима новая характеристика. В данном случае — удельная жесткость — отношение модуля упругости к плотности . Если речь идет о балке, работающей на изгиб, оптимальный критерий выбора материала определяется с учетом поперечного сечения, и соответствует отношению [4]. Для легкой и жесткой пластины соотношение примет вид , так как прогиб будет зависеть от толщины в третей степени. Такой критерий выбора материала называется индексом эффективности. [5]
Диаграммы Эшби
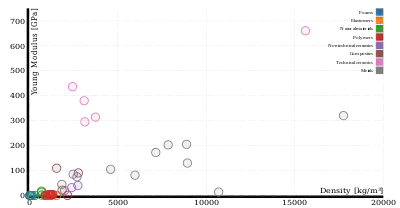
Диаграмма Эшби представляет собой пузырьковую диаграмму, на которой отображены две или более характеристики материалов или классов материалов[5]. Эти диаграммы используются для сравнения соотношений между различными свойствами материалов. Например, для жесткого и легкого стержня, рассмотренного выше, по одной оси необходимо отложить модуль упругости, а по другой — плотность. На саму диаграмму необходимо нанести овалы, характеризующие разброс свойств материалов-кандидатов. На таком графике легко найти не только материал с наибольшей жесткостью, или материал с наименьшей плотностью, но и материал с наилучшим соотношением . Использование логарифмической шкалы по обеим осям может облегчить анализ диаграммы и выбор материала.
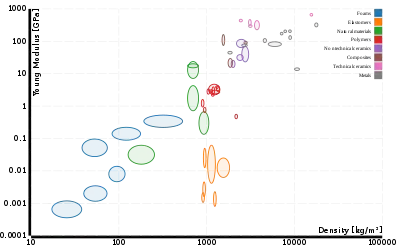
Верхняя диаграмма справа показывает соотношение между модулем упругости и плотностью в линейном масштабе. На диаграмме ниже показаны те же самые свойства материалов в логарифмическом масштабе. Разными цветами показаны разные классы материалов (полимеры, пенопласты, металлы и т.д.)[6].
Так, из-за роста цен на топливо и развития новых технологий, в автомобилестроении сталь заменяют легкими магниевыми и алюминиевыми сплавами, в самолетостроении алюминий заменяют на углепластики и титановые сплавы, а спутники уже давно изготавливаются из экзотических композиционных материалов.
Безусловно, цена за единицу массы материала не является единственным значительным фактором при выборе материала. Важной концепцией является отношение индекса эффективности к стоимости единицы массы материала. Например, если при проектировании легкой и жесткой пластины, описанной выше, добавляется ценовой критерий, то потребуется материал с оптимальным сочетанием плотности, модуля упругости и цены. Данное соотношение свойств можно отразить на диаграмме Эшби — по одной оси откладывается соотношение , по другой — цена за единицу массы.
Оптимизация нескольких сочетаний свойств материалов и ценовых характеристик является сложным процессом, который трудно осуществить вручную. Поэтому существует необходимость в специальном программном обеспечении, которое будет содержать большую библиотеку свойств материалов, информацию об их стоимости, методологию выбора материала и инструменты анализа[7].
Обобщенный метод построения диаграммы Эшби
При построении диаграммы для нескольких сочетаний свойств материалов определяются три различных набора переменных:
- Переменные материала — это свойства, присущие материалу, такие как плотность, модуль упругости, предел текучести и так далее.
- Свободные переменные — величины, которые могут изменятся в процессе проектирования конструкции. Например, в техническом задании не определена длина балки и проектировщик может ее изменять по своему усмотрению.
- Фиксированные переменные — это ограничения, налагаемые на конструкцию. Например, строго определенная толщина балки или установленный допустимый прогиб.
Из этих переменных выводится уравнение для индекса эффективности. Это уравнение является критерием выбора материала и количественно определяет, насколько эффективным будет использование материала для конкретного применения. Полученный индекс эффективности наносится на диаграмму. Анализ диаграммы позволяет определить выбор какого материал является наиболее эффективным. Как правило, высокий индекс эффективности показывает более эффективное применение материала.
Пример использования диаграммы Эшби
В этом примере материал подвергается воздействию растяжения и изгиба. Целью выбора материала является определение материала, который будет хорошо работать в обоих случаях нагружения.
Индекс эффективности при растяжении
В первой ситуации на стержень воздействует собственный вес и растягивающая сила . Переменными материала являются плотность и напряжения Предположим, что длина и растягивающая сила определены в техническом задании, в таком случае они являются фиксированными переменными. Наконец, площадь сечения - свободная переменная. В данной постановке целью является минимизация массы путем выбора материала с оптимальным сочетанием переменных материала — . Рисунок 1 иллюстрирует данную задачу.

Напряжение в стержне определяется соотношением , а масса соотношением . Для получения индекса эффективности необходимо убрать из соотношения все свободные переменные, оставив только фиксированные переменные и переменные материала. В данном случае из соотношения необходимо убрать площадь . Уравнение напряжения при растяжении можно выразить как . При подстановке полученного в соотношение для массы получим . Далее переменные материала и фиксированные переменные группируются отдельно: .
Переменные и можно убрать из конечного соотношения так как они являются фиксированными и их нельзя изменять в процессе проектирования. В таком случае целевое соотношение примет вид . Поскольку целью является уменьшение массы , то полученное соотношение также должны быть сведено к минимуму. Однако, принято, что индекс эффективности является параметром, который максимизируют. Поэтому индекс эффективности примет вид .
Индекс эффективности при изгибе
Во второй ситуации материал подвергается воздействию изгибающих моментов. Уравнение максимальных напряжений при изгибе имеет вид , где — изгибающий момент, — расстояние от нейтральной оси, — момент инерции сечения. Схема приложения нагрузки изображена на рисунке 2. Используя приведенное выше соотношение для массы и решив его для свободных переменных, получится соотношение , где — длина, а — высота балки. Если , , и — фиксированные переменные, то индекс эффективности при изгибе имеет вид .

Выбор наилучшего материала для двух случаев нагружения
Получено два индекса эффективности: для случая растяжения и для случая изгиба . Первым шагом необходимо построить диаграмму Эшби, где в логарифмических масштабах отложить по одной из осей плотность, а по другой — прочность и нанести свойства материалов, подвергаемых анализу.
Для случая растяжения первым шагом является извлечение логарифма из обеих частей соотношения. Полученное уравнение можно представить как . Соотношение имеет вид . Это означает, что соотношение линейно при отображении в логарифмическом масштабе. Точка пересечения с осью y — это логарифм . Если отложить эту линию на диаграмме Эшби, то все материалы, через которые проходит эта линия имеют одинаковый индекс эффективности. Чем выше положение линии по оси y, тем выше индекс эффективности. В примере значение принято равным 0.1, таким образом, чтобы линия проходила через материал с наивысшим индексом эффективности — карбидом бора (рисунок 3).
Используя степенные свойства логарифмов соотношение для изгиба можно преобразовать аналогичным образом. Соотношение примет вид . Используя подход, описанный в абзаце выше, получим, что для изгиба составляет ≈ 0,0316 (рисунок 3).

Из анализа диаграммы видно, что наибольший индекс эффективности для случая растяжения приходится на карбид бора; для случая изгиба — на пенопласты и карбид бора. Таким образом, наилучшим материалом, работающим в условиях растяжения и изгиба, является карбид бора. Однако, технические керамики являются достаточно дорогими материалами. Принимая во внимание этот факт, наилучшим вариантом будет являться материал, с меньшим показателем индекса эффективности, но более дешевый — углепластик (CFRP).
Примечания
- Dieter, George E.,. Engineering design. — 4th ed. — Boston: McGraw-Hill Higher Education, 2009. — С. 460. — 956 с. — ISBN 978-0-07-283703-2.
- Christian Okafor, Alex Tagbo, Obiora Obiafudo, Emmanuel Nwadike. Material Selection and Fluid Flow Analysis of Parallel Flow Heat Exchanger // Archives of Current Research International. — 2016-01-10. — Т. 6, вып. 3. — С. 1—14. — doi:10.9734/ACRI/2016/30239.
- General Considerations of Machine Design Архивная копия от 15 апреля 2019 на Wayback Machine, Mechanical Engineering Community & Discussion, retrieved 2018-04-15.
- Чумак П. И., Кривокрысенко В. Ф. Расчет, проектирование и постройка сверхлегких самолетов / Ред. М. Е. Орехова.. — М.: Патриот, 1991. — С. 87. — 238 с.
- Ashby, Michael Materials Selection in Mechanical Design (неопр.). — 3rd. — Burlington, Massachusetts: Butterworth-Heinemann, 1999. — ISBN 0-7506-4357-9.
- Ashby, Michael F. Materials Selection in Mechanical Design (неопр.). — USA: Elsevier Ltd., 2005. — С. 251. — ISBN 978-0-7506-6168-3.
- M. B. Babanli, F. Prima, P. Vermaut, L. D. Demchenko, A. N. Titenko. Material Selection Methods: A Review // 13th International Conference on Theory and Application of Fuzzy Systems and Soft Computing — ICAFS-2018 / Rafik A. Aliev, Janusz Kacprzyk, Witold Pedrycz, Mo. Jamshidi, Fahreddin M. Sadikoglu. — Cham: Springer International Publishing, 2019. — Т. 896. — С. 929—936. — ISBN 9783030041632, 9783030041649. — doi:10.1007/978-3-030-04164-9_123.