Булевы операции над многоугольниками
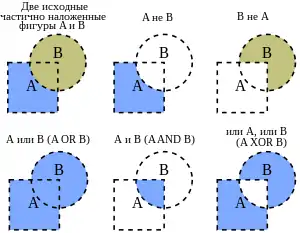
Бу́левы опера́ции над многоуго́льниками и́ли фигу́рами — это набор булевых операций (AND, OR, NOT, XOR, ...) с одним или несколькими наборами многоугольников в компьютерной графике. Эти наборы операций широко используются в компьютерной графике, САПР и в проектировании электронных схем (физическое расположение элементов интегральных схем и программы проверки).
Алгоритмы
- Алгоритм отсечения Грайнера – Хорманна
- Алгоритм отсечения Ватти
- Алгоритм Сазерленда – Ходжмана (алгоритм для частного случая)
- Алгоритм Уайлера — Атертона (алгоритм для частного случая)
Применение в программировании
Ранние алгоритмы булевых операций с многоугольниками основывались на битовых картах. Использование битовых карт в моделировании многоугольных фигур и операциях над ними имеет много недостатков. Один из недостатков — может потребоваться очень много памяти, поскольку разрешение рисунка многоугольника пропорционально числу пикселей, используемых для представления многоугольников. Чем больше разрешение изображения, тем большее число бит требуется хранить в памяти.
Современная воплощение булевых операций над многоугольниками использует алгоритмы заметания плоскости (или алгоритмы заметающей прямой). Список статей, использующих алгоритм заметающей прямой для булевых операций над многоугольниками, можно найти ниже в списке литературы.
Булевы операции над выпуклыми многоугольниками и монотонными многочленами с одинаковыми направлениями можно осуществить за линейное время[1].
См. также
- Алгебра логики
- Вычислительная геометрия
- Конструктивная сплошная геометрия
- General Polygon Clipper (Общее Отсечение Многоугольника), библиотека на C, вычисляющая результат операции отсечения
- Конструктивная сплошная геометрия, метод определения трёхмерных фигур с использованием аналогичных операций
Примечания
- Katz, Overmars, Sharir, 1992, с. 223–234.
Литература
- Matthew J. Katz, Mark H. Overmars, Micha Sharir. Efficient hidden surface removal for objects with small union size // Computational Geometry (journal). — 1992. — Т. 2, вып. 4. — С. 223–234. — doi:10.1016/0925-7721(92)90024-M.
- Mark de Berg, Marc van Kreveld, Mark Overmars, Otfried Schwarzkopf. Algorithms and Applications. — Second Edition. — 2000.
- Jon Louis Bentley, Thomas A. Ottmann. Algorithms for Reporting and Counting Geometric Intersections // IEEE Transactions on Computers. — 1979. — Т. C-28, вып. 9. — С. 643–647.
- Jon Louis Bentley, Derick Wood. An Optimal Worst Case Algorithm for Reporting Intersections of Rectangles // IEEE Transactions on Computers. — 1980. — Т. C-29, вып. 7. — С. 571–577.
- Ulrich Lauther. 18th Design Automation Conference. — 1981. — С. 555–562.
- James A. Wilmore. 18th Design Automation Conference. — 1981. — С. 571–579.
- J. Nievergelt, F. P. Preparata. Plane-Sweep Algorithms for Intersecting Geometric Figures // Communications of the ACM. — 1982. — Т. 25, вып. 10. — С. 739–747. — doi:10.1145/358656.358681.
- =Thomas Ottmann, Peter Widmayer, and Derick Wood. Computer Vision, Graphics, and Image Processing. — 1985. — Т. 30. — С. 249–268.
Ссылки
- UIUC Computational Geometry Pages
- Constructive planar geometry, by Dave Eberly.
- Алгоритмы и программы
- Михаил Леонов составил сравнение алгоритмов отсечения многоугольников.
- Ангус Джонсон составил также сравнение трёх библиотек отсечения.
- Компания SINED GmbH составила сравнение производительности и использования памяти трёх алгоритмов отсечения.
- Сравнение 5 библиотек отсечения rogue-modron.blogspot.com
- Коммерческая библиотека для 3-мерных булевых операций: sgCore C++/C# Библиотека.
- comp.graphics.algorithms FAQ, решения математических задач с 2D- и 3D-многоугольниками.
- gfxpoly Маттиаса Крамма, свободно распространяемая библиотека на C для 2D-многоугольников (лицензия BSD).
- Библиотека Boolean Клааса Холверда, C++ библиотека для 2D-многоугольников.
- Polypack Дэвида Кеннисона, библиотека на Фортране, основанная на алгоритме Ватти.
- Clippoly Кламера Шатте, программа отсечения многоугольника, написанная на C++.
- poly_Boolean Михаила Леонова, C++ library, расширяющая алгоритм Шатта.
- Clipper Ангуса Джонсона, свободно распрстраняемая библиотека с открытым кодом (написанная на Delphi, C++ и C#), основанная на алгоритме отсечения Ватти.
- GeoLib, коммерческая библиотека, доступная на C++ и C#.
- GPC Алана Марта, библиотека «Общее Отсечение Многоугольника».
- PolygonLib, C++ и COM библиотеки для 2D-многоугольников (оптимизирована для больших множеств многоугольников, встроенный пространственный индекс).