Ациклическая ориентация

Любой граф имеет ациклическую ориентацию. Одним из способов создания ациклических ориентаций является упорядочение вершин с последующим ориентированием каждого ребра от более ранней вершины в списке к более поздней. Последовательность вершин тогда становится топологическим упорядочиванием получившегося ориентированного ациклического графа (ОАГ) и любая топологическая сортировка этого ОАГ образует одну и ту же ориентацию.

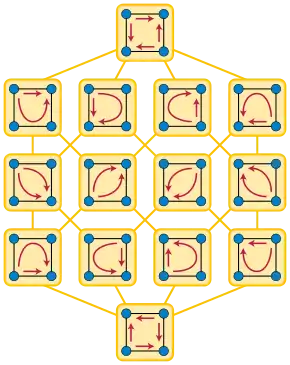
Поскольку любой ОАГ имеет топологическую сортировку, любая ациклическая ориентация может быть получена указанным образом. Однако различные последовательности вершин могут привести к одинаковым ациклическим ориентациям, если получаемый ОАГ имеет несколько топологических сортировок. Например, у цикла с четырьмя вершинами (показан на рисунке) существует 24 различных последовательности, но только 14 возможных ациклических ориентаций.

Теорема Галлаи – Хассе – Роя – Витавера утверждает, что граф имеет ациклическую ориентацию, в которой максимальный путь имеет не более k вершин, тогда и только тогда, когда граф может быть раскрашен не более чем в k цветов [1].

Число ациклических ориентаций можно посчитать, используя хроматический многочлен ${\displaystyle \chi _{G}}$, значение которого для положительного целого числа k равно числу k-раскрасок графа. Любой граф G имеет в точности ${\displaystyle |\chi _{G}(-1)|}$ различных ациклических ориентаций [2], так что в этом смысле ациклические ориентации можно понимать как раскраску с −1 цветом.

Для планарных графов ациклические ориентации являются двойственными вполне циклическим ориентациям, ориентациям, в которых каждое ребро принадлежит ориентированному циклу — если ${\displaystyle G}$ является планарным графом, и ориентации ${\displaystyle G}$ переводятся в ориентации двойственного графа ${\displaystyle G}$ путём поворота каждого ребра на 90 градусов по часовой стрелке, то вполне циклическая ориентация графа ${\displaystyle G}$ соответствует полученной таким образом ациклической ориентации двойственного графа, и наоборот [3].

Подобно хроматическому многочлену, многочлен Татта ${\displaystyle T_{G}}$ графа ${\displaystyle G}$ можно использовать для подсчёта числа ациклических ориентаций ${\displaystyle G}$ как ${\displaystyle T_{G}(2,0)}$. Двойственность между ациклическими и вполне циклическими ориентациями планарных графов можно распространить тем же образом на непланарные графы — многочлен Татта двойственного графа планарного графа получается обменом аргументов многочлена ${\displaystyle T_{G}}$ и число вполне циклических ориентаций графа ${\displaystyle G}$ равно ${\displaystyle T_{G}(0,2)}$, что получается обменом аргументов в формуле для числа ациклических ориентаций[4].

Множеству ациклических ориентаций заданного графа может быть дана структура частичного куба, в котором две циклические ориентации смежны, если они отличаются направлением только одного ребра[5]. Из этого следует, что если две различные ациклические ориентации одного и того же графа различаются направлением k рёбер, можно преобразовать одну из ориентаций в другую последовательностью k изменений ориентации одного ребра, так что каждое промежуточное состояние является ациклической ориентацией.

Полидерево, результат ациклической ориентации дерева

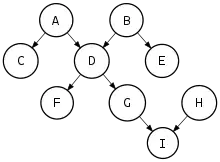
Любая ориентация дерева ациклична. Ориентированный ациклический граф, полученный такой ориентацией называется полидеревом[6].

Ациклическая ориентация полного графа называется транзитивным турниром и она эквивалентна полному упорядочению вершин графа. В такой ориентации существует, в частности, в точности один источник и один сток.

Ациклическая ориентация произвольного графа, имеющая единственный источник и единственный сток, называется биполярной ориентацией [7].

Транзитивная ориентация графа является ациклической ориентацией, которая является его транзитивным замыканием. Не любой граф обладает транзитивной ориентацией. Графы, имеющие транзитивную ориентацию, являются графами сравнимости[8]. Полные графы являются частным случаем графов сравнимости, а транзитивные турниры являются частным случаем транзитивных ориентаций.