Ауксетики

Ауксетики (от греч. αὐξητικός) — материалы, имеющие отрицательные значения коэффициента Пуассона. Термин введен профессором Кеном Эвансом (Ken Evans) из Эксетерского университета.[1]

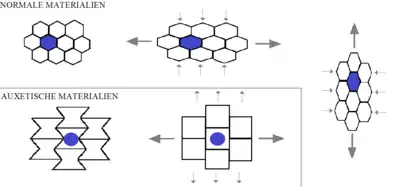
При растяжении материалы-ауксетики становятся толще в направлении, перпендикулярном приложенной силе. Это происходит из-за шарнирно-подобной структуры ауксетиков, которая деформируется при растяжении. Такое свойство может обусловливаться свойствами отдельных молекул или определяться структурными особенностями материала на макроскопическом уровне. От материалов этого типа ожидаются хорошие механические свойства, такие как значительное поглощение механической энергии и высокое сопротивление разрушению.

Ученым известны материалы с подобными свойствами уже около 100 лет[2], но в настоящее время им уделяют повышенное внимание. Один из первых синтетических ауксетиков был описан в 1987 году в статье под названием «Foam structures with a Negative Poisson’s Ratio» («Пенные структуры с отрицательным коэффициентом Пуассона»).[3]

Конструкция с отрицательным коэффициентом Пуассона была предсказана еще в 1985 году, [4] [5] когда были опубликованы проекты материалов с ячейками периодичности в виде "вывернутых" пчелиных сот.

Ауксетиками являются

• Некоторые горные породы и минералы(например пирит);[2]
• Кристаллические материалы: Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn, Sr, Sb, MoS${\displaystyle _{2}}$ и другие.[6][7]
• Углеродные алмазоподобные фазы[8]
• Неуглеродные трубки[9][10]
• Живые костные ткани (предположительно);
• Определенные варианты полимеров политетрафторэтилена, такие как Gore-Tex;[11]
• Бумага.[12]
• Органические цепные молекулы. Недавние исследования показали, что такие органические кристаллы, как н-парафины и подобные им, могут демонстрировать ауксетическое поведение. [13]