Алгоритм Diamond-Square

Алгоритм Diamond-Square — метод генерации карт высот для компьютерной графики.

Идея впервые была введена Фурнье, Фусселем и Карпентером на конференции siggraph 1982[1]. Он был позже проанализирован Гэвином Миллером на конференции siggraph-1986[2], Миллер описал в алгоритме ряд недостатков, таких как «складки», возникающие на краях карты.

Алгоритм начинает работу с 2D сетки, затем, из четырёх начальных значений, случайным образом генерирует карту высот, упорядоченную в виде сетки из точек так, чтобы вся плоскость была покрыта квадратами.

Алгоритм

Алгоритм diamond-square начинает работу с двумерного массива размера 2n + 1. В четырёх угловых точках массива устанавливаются начальные значения высот. Шаги diamond и square выполняются поочередно до тех пор, пока все значения массива не будут установлены.

Шаг diamond. Для каждого квадрата в массиве, устанавливается срединная точка, которой присваивается среднее арифметическое из четырёх угловых точек плюс случайное значение.

Шаг square. Берутся средние точки граней тех же квадратов, в которые устанавливается среднее значение от четырёх соседних с ними по осям точек плюс случайное значение.

Случайное число обычно выбирается в промежутке [-Ri, Ri], где R это фактор неровности (roughness factor) в промежутке от 0 до 1, а i это номер итерации (шаг diamond и шаг sqare это одна итерация). Соответственно, при каждой итерации случайное значение, прибавляющееся к срединным точкам, уменьшается.

В шагах diamond, точки, расположенные по краям общего массива будут иметь только три соседних значения а не четыре (четвертая точка будет выходить за размерность массива). Есть несколько способов справиться с этим — самое простое, взять среднее от трех крайних точек. При последовательном использовании с указанием общих начальных значений, этот метод позволяет «сшивать» генерируемые карты высот.

Визуализация

На рисунке ниже показаны шаги, проходимые алгоритмом diamond-square на примере массива 5х5.

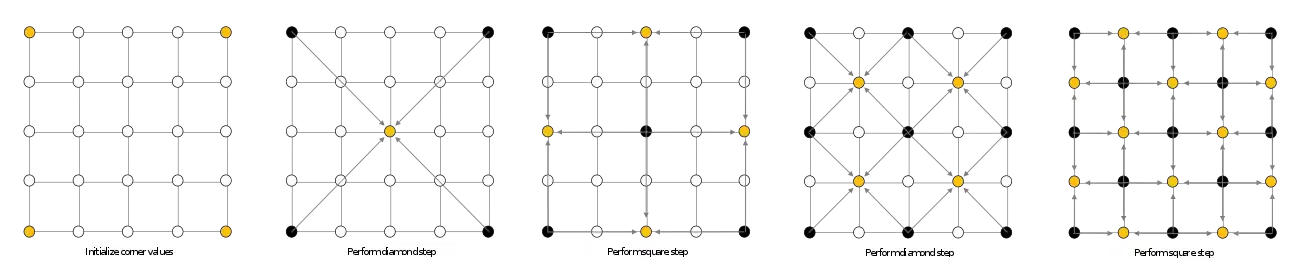
Шаг 1. Инициализация угловых точек. Присваивание им значений высот (например, выбором случайных чисел).

Шаг 2. Шаг diamond. Нахождение срединной точки, присваивание ей значения, на основе среднего от угловых, плюс случайное число.

Шаг 3. Шаг square. Нахождение срединных точек для ромбов отмеченных черными точками (на этом шаге, по одной точке каждого ромба выходят за пределы массива). Плюс случайное число.

Шаг 4. Шаг diamond. Для каждого квадрата (на этом шаге их 4), повторяем шаг № 2.

Шаг 5. Шаг square. Повторяем шаг № 3 для каждого ромба. У ромбов, имеющих точки на краю массива, одна из точек выходит за пределы массива.

Приложения

Этот алгоритм может быть использован для генерации реалистичных ландшафтов. Различные реализации используются в компьютерных графических программах, например terragen.

Примечания
  1. Fournier, Alain; Fussell, Don; Carpenter, Loren (June 1982).
  2. Miller, Gavin S. P. (August 1986).

Ссылки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.