SOBER-t32
SOBER-t32 (англ. Seventeen Octet Byte Enabled Register) — cинхронный аддитивный потоковый шифр из семейства SOBER. Авторами являются Филип Хаукес и Грегори Роуз (Австралия).
| SOBER-t32 | |
|---|---|
| Создатель | Филип Хаукес и Грегори Роуз |
| Создан | 2000 год |
| Опубликован | 2000 год |
| Размер ключа | 256 бит |
| Тип | Поточный шифр |
Историческая справка
SOBER — семейство потоковых шифров, широко используемых во встроенных системах, предложенное Г. Роузом в 1998 году. На данный момент семейство включает в себя шифры SOBER[1], SOBER-II[2], S16, S32[3], SOBER-t8, SOBER-t16[4], SOBER-t32[5] и SOBER-128[6].
Первый программный потоковый шифр из семейства был разработан с целью удовлетворения основных требований встроенных приложений, которые накладывают жёсткие ограничения на объём вычислительной мощности, программного пространства и памяти, доступной для программных алгоритмов шифрования. Шифрование речи для беспроводной телефонии — одна из первых и главных сфер применения шифров SOBER. Так как большинство используемых мобильных телефонов представляют собой микропроцессор и память, быстрый программный потоковый шифр, использующий небольшое количество памяти, является наиболее подходящим вариантом для таких приложений. Многие методы генерации потока псевдослучайных битов основаны на регистрах сдвига с линейной обратной связью (РСЛОС) над конечным полем Галуа порядка 2. Такие шифры неэффективно использовать на ЦПУ. Шифры семейства SOBER обходят данную проблему, используя РСЛОС над полем и ряд методов, позволяющих значительно увеличить скорость генерации псевдослучайной последовательности в программном обеспечении на микропроцессоре.[7]
Стремление усилить безопасность и использовать шифр в 16-битных и 32-битных процессорах привело к возникновению нескольких вариантов первоначального шифра SOBER. Однако, когда в нём были обнаружены различные недостатки, он был заменён на SOBER-II и его дополнения — S16 и S32. S16 копирует структуру SOBER II и является расширением данного алгоритма до 16-битной арифметики. В это же время S32 основан на 32-битной арифметике[7][8], а структура данного шифра отлична от SOBER-II и S16. Тем не менее, при последующем анализе SOBER-II были обнаружены атаки, которые выявили недостаток всей структуры шифра, а не его отдельных частей. Как итог, на замену существующим шифрам были выпущены три новые версии, основанные на 8-битной, 16-битной и 32-битной арифметике, называемые t-классом шифров SOBER. Синхронные потоковые шифры SOBER-t16 и SOBER-t32 были представлены в программе NESSIE.[9] И хотя оба шифра в итоге были признаны не соответствующими строгим требованиям NESSIE, согласно заключительному отчёту о безопасности, выпущенному NESSIE в феврале 2003 года, на втором этапе отбора были рассмотрены только четыре потоковых шифра: BMGL, SNOW, SOBER-t16 и SOBER-t32.
Описание алгоритма
SOBER-t32 — это 256-битный синхронный потоковый шифр из семейства SOBER. В шифрах данного типа ключи генерируются независимо от открытого текста. Для того чтобы зашифровать открытый текст, отправитель выполняет операцию XOR между открытым текстом и потоком ключей. Если получателю известен секретный ключ, то он может восстановить поток ключей и расшифровать сообщение, выполнив операцию XOR между зашифрованным текстом и потоком ключей.[10]
Основными элементами шифрообразующего устройства являются[11]:
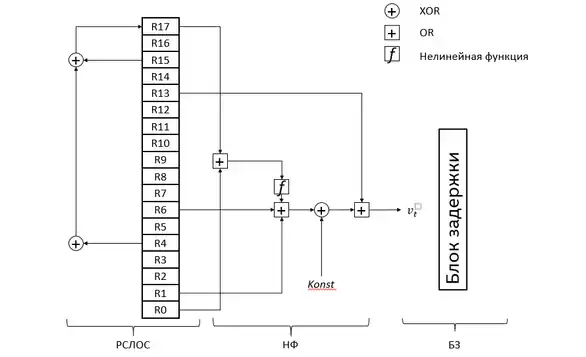
- Регистр сдвига с линейной обратной связью (РСЛОС), который использует рекуррентное соотношение для создания последовательности состояний (слов) .
- Нелинейный фильтр (НФ) — создаёт поток из , создавая нелинейную комбинацию из полученных слов.
- Блок «задержки», или «усечения» (БЗ) — генерирует поток ключей , прорежая НФ-поток нерегулярным образом.
Элементы представлены над полем Галуа с использованием базиса . Если , то представим как , где . Работа шифра основана на 32-битных операциях над по модулю полинома вида:
Сложение двух элементов в представляется как сложение соответствующих полиномов с приведением коэффициентов по модулю два. Умножение двух элементов в представляется как умножение соответствующих полиномов с приведением коэффициентов полиномов по модулю два. Результат умножения затем приводится по модулю неприводимого полинома .[13]
Регистр сдвига с линейной обратной связью (РСЛОС)
РСЛОС — сдвиговый регистр длины 17, где каждая ячейка содержит одно 32-разрядное слово. Таким образом, полная внутренняя память составляет 544 бит. Состояние РСЛОС в момент времени задаётся вектором:
Следующее состояние РСЛОС получается путём сдвига предыдущего состояния на один шаг. Новое слово вычисляется как линейная комбинация слов, содержащихся в РСЛОС, по следующему правилу:
где , — исключающее или (XOR).
Нелинейный фильтр (НФ)
Нелинейный фильтр предназначен для уменьшения вероятности успешного криптоанализа шифра. Основная цель НФ — скрыть линейность выходного потока регистра[15]. В каждый момент времени нелинейный фильтр берёт из РСЛОС пять слов и вычисляет значение, обозначаемое :
где:
- — сложение по модулю .
- константа — слово, которое определяется во время инициализации РСЛОС и сохраняется до конца сеанса.
- задаёт некоторую нелинейную функцию.
Функция используется для достижения нескольких целей. Во-первых, она скрывает линейность в младшем значащем бите (eng. Least Significant Byte или LSB) и добавляет значительную нелинейность в оставшиеся биты. Во-вторых, она гарантирует, что результат сложения и не коммутирует с результатом сложения и . В-третьих, обеспечивает, чтобы каждый бит вывода НФ зависел от каждого бита и . Операция XOR с константой в рассматриваемой формуле используется для двух целей. В первую очередь данное действие увеличивает сложность любой атаки (исключая полный перебор), поскольку имеется 216 возможных функций НФ.[15] Вдобавок, добавляется к выражению через XOR для того, чтобы снизить вероятность коммутации прибавления и сложения и . Несмотря на это, все ещё существует небольшая вероятность того, что операции будут коммутировать. Однако, эта вероятность мала и зависит от значения .[17]
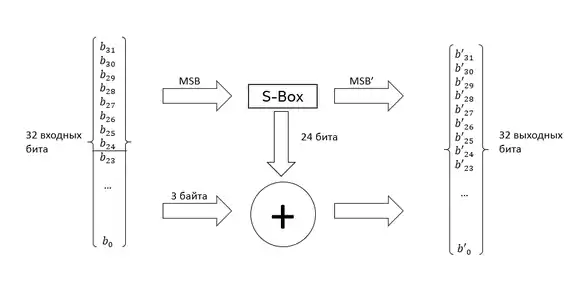
Внутри функции слово разбивается на старший значащий байт (eng. Most Significant Byte или MSB) и три оставшихся байта. MSB подаётся на вход блока замещения[18](eng. Substitution Box or S-box), который генерирует 32 бита. В этом 32-битном выходе MSB совпадает с MSB исходного слова, а операция XOR между тремя оставшимися байтами и аналогичной частью исходного слова формирует оставшуюся часть выходного слова. Таким образом, функция представима в виде:
где — старший значащий байт слова , а представляет собой оставшуюся часть входного слова.
Блок задержки (БЗ)
Блок задержки нерегулярно «прореживает» поток, идущий из НФ, чтобы затруднить восстановление состояния шифрообразующего устройства, например, путём корреляционной атаки. Суть заключается в том, что случайные слова из нелинейного вывода используются для определения включения других слов в выходной поток. Первое 32-разрядное слово на выходе НФ является первой командой управления усечением (eng. Stutter Control Word или SCW)[20]. Каждый бит данного управляющего слова разбивается на пары бит, называемые дибитами. Наборы дибитов предоставляют шифру различные инструкции — сколько циклических проходов по РСЛОС необходимо сделать, подавать ли вывод НФ на выход, как вставить этот вывод в конечный ключевой поток. После использования всех дибитов новое SCW берётся из вывода НФ. Правила определены следующим образом[21]:
- 00 — следующее слово будет исключено из потока ключей;
- 01 — в поток ключей идёт результат операции XOR между следующим словом и константой , последующее слово удаляется из потока ключей;
- 10 — следующее слово исключается, а слово за ним попадает в ключевой поток;
- 11 — в поток ключей идёт результат операции XOR между следующим словом и константой .
Здесь , а — побитовое дополнение .
Использование данного механизма позволяет пропустить в ключевой поток только около 48 % слов потока НФ.[22]
Атаки на SOBER-t32
«Предполагай и определяй» атака на SOBER-t32 без блока задержки
В стандартной атаке «Предполагай и определяй» (англ. Guess and determine attack) угадываются некоторые слова регистра РСЛОС, а оставшиеся слова определяются путём использования уравнений на РСЛОС и НФ. Данная атака может быть успешна проведена только в том случае, если шифрообразующее устройство не содержит блок задержки. Он предотвращает атаку — не столько из-за неопределённости, которую он вносит, сколько из-за того, что последовательные слова не появляются в конечном ключевом потоке.[22]
Упрощённая схема: биты переноса известны
В данной секции рассмотрен упрощённый вид атаки, в котором биты переноса известны заранее. Распишем выражение для выхода НФ с учётом явного вида функции , рассматривая старший значащий байт и остальные байты отдельно:
где обозначает бит переноса, идущий к MSB. Предполагая, что MSB константы равен нулю, это уравнение можно разбить на две отдельные части:
В данной системе SBOX1 представляет собой старший значащий байт выходного сигнала блока замещения, а SBOX2 — три оставшихся байта этого выхода. обозначает биты переноса представленных операций сложения. Наиболее интересным является первое выражение представленной системы. Зная старшие значащие биты слов , потока ключей и значения битов переноса и , появляется возможность рассчитать старший значащий бит слова .
В данной подсекции рассматривается случай, когда биты переноса не учитываются. Таким образом, на первом этапе атаки необходимо угадать только старшие значащие биты первых 16 слов РСЛОС (, , …, ) — в общей сложности 128 бит. Зная их и поток ключей , можно вычислить MSB для следующих слов , , и т. д. Остаётся предсказать младшие 24 бита каждого слова, которые появляются в РСЛОС. Их можно извлечь из системы линейных уравнений, получаемых после каждой итерации работы шифратора:
- 32 линейных уравнения на основании вывода нового слова из РСЛОС.
- Дополнительное линейное уравнение на младший значащий бит. Так как входные данные для S-box известны, то для младшего значащего бита имеет место следующее выражение:
Таким образом, после срабатываний РСЛОС генерируется линейных уравнения, в которых неизвестными являются:
- 24 младших значащих бита изначальной последовательности , , …, .
- значение младшего значащего бита константы .
- 24 младших значащих бита нового слова на каждой последующей итерации.
Всего неизвестных. Для того чтобы система была разрешима, число переменных не должно превышать число уравнений, то есть:
Важно отметить, что атака восстанавливает полное состояние шифра, за исключением 23 оставшихся бит константы . Однако после завершения атаки эти биты легко восстанавливаются из второго уравнения системы.
Для оценки сложности атаки необходимо знать число бит, которые требуется угадать. В данной версии, следующие биты должны быть угаданы:
- MSB первых 16 слов РСЛОС — 128 бит.
- MSB константы K — 8 бит.
В общей сложности для успешной атаки необходимо угадать 136 бит, что подразумевает сложность . В следующем разделе будет представлена сложность полной атаки, учитывающей также и биты переноса.[23]
Полная атака
Предыдущий раздел базируется на упрощении, что биты переноса известны заранее. В действительности их также необходимо угадывать. При этом биты переноса не являются чисто случайными, распределение их значений неравномерно.[24] Этим можно воспользоваться при атаке — вначале попытаться угадать наиболее вероятные значения. Среднее число угадываний хорошо аппроксимируется энтропией, поскольку она равна количеству информации, которая присутствует в битах переноса. Энтропии битов переноса и могут быть получены теоретически — равны 1 и 1.65 соответственно.[25][26]
Для совершения атаки необходимо угадать:
- 136 бит — из предыдущего раздела.
- Биты переноса — всего бит.
Таким образом, сложность полной атаки есть
Атака-различитель
В криптографии атакой-различителем (eng. Distinguishing attack) называется любая форма криптоанализа некоторых зашифрованных данных, которая позволяет злоумышленнику выделить зашифрованные данные из потока случайных. Современные шифры с симметричным ключом специально разработаны для защиты от таких атак. Другими словами, современные схемы шифрования являются псевдослучайными перестановками и предназначены для «размывания» зашифрованного текста. Если найден алгоритм, который может отличить выходной поток шифра от случайного быстрее, чем полный перебор, то шифр считается взломанным.
Атаки-различители показывают, что блок задержки не может сорвать все атаки, основанные на знании большой части ключевого потока. Однако и сам блок задержки является неимоверно затратным средством, поскольку снижает производительность шифра на 52 %.[22]
На конференции FSE в 2002 году, П. Экдал и Т. Джонсон представили вариант атаки-различителя на SOBER-t32 без блока задержки, который может быть расширен и на полную схему.[27]
Атака на SOBER-t32 без блока задержки
Атака начинается с линеаризации выхода НФ:
Шум , возникающий вследствие данной аппроксимации, имеет смещённое распределение.[29] Возводя в квадрат выражение для получения нового слова из РСЛОС, получим новое линейное рекуррентное соотношение:
где .
После этого считается XOR между соседними битами в потоке :
Затем рассчитывается распределение для значений . Согласно результатам моделирования это распределение достаточно смещено. Наибольшее смещение было обнаружено у значений, получаемых на 29-ом и 30-ом битах. Смещение зависит от соответствующих битов и для битов 29 и 30 составляет не менее [30]
Теперь, имея поток из НФ , можно воспользоваться введённым ранее рекуррентным выражением для подсчёта:
где сумма всех по определению равна нулю. Таким образом, данное выражение может быть переписано в следующем виде:
Обозначим левую часть верхнего выражения как , а правую — . Теперь возможно рассчитать следующую вероятность:
где обозначает смещение. Используя эту формулу, можно получить финальное значение вероятности корреляции шести независимых позиций в потоковом ключе для :
Для того чтобы отличить данное неравномерное распределение от равномерного источника , между двумя распределениями вычисляется информация Чернова[31]:
Чтобы получить вероятность ошибки , необходимо выборок из ключевого потока. Каждая выборка состоит из бит, поэтому всего необходимо слов из потока НФ, чтобы отличить SOBER-t32 (без блока задержки) от остального потока из единого источника.
Атака на полную версию SOBER-t32
Данная версия основывается на знании слов из потока НФ. Необходимо отыскать эти слова в потоке ключей , то есть уже после прохождения блока задержки. Прежде всего высчитывается вероятность того, что конкретное слово будет найдено в своей наиболее вероятной позиции в потоке ключей. Берётся слово из потока ключей, которое происходит от конкретного слова из потока НФ. Затем вычисляется вероятность того, что последующие слова появятся в своих наиболее вероятных положениях в ключевом потоке.
По статистике наиболее вероятной позицией для в потоке ключей является , для — . Согласно результатам симуляций вероятности найти данные слова в таких положениях в потоке ключей составляют 21,7 % и 19,8 % соответственно.[32] Для остальных трёх слов необходимы более сложные теоретические выкладки. Для -го слова, поступающего в блок задержки, можно ожидать, что слов управления задержкой (SCW) использовались ранее. Также ожидается, что из всех оставшихся (не SCW) слов 50 % в конечном счёте попадут в поток ключей. При этом наиболее вероятная позиция для слова :
Вероятность найти слово в данной наиболее вероятной позиции рассчитывается, исходя из вероятности того, что -ое слово управления задержкой появится в своей наиболее вероятной позиции в потоке НФ. Эту вероятность легче рассчитать теоретически, и легко увидеть, что асимптотическое поведение обоих значений будет одинаковым.[33]
Ранее вводилось, что два дибита — 00 и 11 — определяют, что произойдёт со следующим словом. Два других дибита — 01 и 10 — определяют задержку двух следующих слов. Поскольку каждый дибит появляется с одинаковой вероятностью, ожидается, что один дибит в среднем использует 1.5 слова из потока НФ. SCW выдаёт 16 дибитов и, таким образом, использует в среднем 24 слова. Поскольку SCW также поступает из потока НФ, ожидается, что -й SCW находится на позиции потока НФ. Вероятность того, что данный SCW действительно находится в этой позиции, равна вероятности того, что слов управления задержкой определят задержку ровно слов из потока НФ. Это означает, что половина из дибитов должна определять задержку одного слова, а другая половина — задержк
у двух слов. Эта вероятность может быть рассчитана следующим образом:
С помощью формулы Стирлинга верхнее выражение упрощается:
Вероятность же нахождения следующих слов в потоке ключей в своих наиболее вероятных позициях задаётся следующим образом:
где — константа (значение получено экспериментально).[34]
Используя данную формулу, можно рассчитать вероятности для слов . Они — при условии, что предыдущие слова находятся в ключевом потоке в их наиболее вероятном положении — равны соответственно. Таким образом, слова присутствуют в итоговом потоке ключе в своих наиболее вероятных позициях равна:
Теперь, аналогично предыдущему пункту, можно рассчитать информацию Чернова и количество слов, необходимых для атаки:
где — распределение НФ-потока. Для достижения ошибки в необходимо выборок — для атаки потребуется последовательностей из слов из потока ключей, всего слов.
Примечания
- SOBER, 1998.
- SOBER II, 1998.
- S16 & S32, 2000.
- SOBER-t, 1998.
- SOBER-t32 specification, 2000.
- SOBER 128, 2003.
- SOBER-t, 1998, p. 2.
- SOBER Family, 2011, p. 1.
- SOBER-t: probabilistic factors, 2002, p. 1.
- SOBER-t, 1998, pp. 1-3.
- Cryptanalysis of SOBER-t32, 2003, pp. 2-3.
- SOBER-t: probabilistic factors, 2002, уравнение 3, p. 2.
- SOBER-t, 1998, pp. 4-5.
- SOBER-t: probabilistic factors, 2002, уравнение 6, p. 3.
- SOBER Family, 2011, p. 2.
- SOBER-t: probabilistic factors, 2002, уравнение 7, p. 3.
- DA, 2002, p. 215.
- SOBER-t, 1998, pp. 1-2.
- SOBER-t, 1998, p. 8.
- Cryptanalysis of SOBER-t32, 2003, p. 4.
- DA, 2002, Таблица 1, p. 215.
- Cryptanalysis of SOBER-t32, 2003, p. 14.
- Cryptanalysis of SOBER-t32, 2003, pp. 7-12.
- SOBER-t: probabilistic factors, 2002, pp. 7-8.
- SOBER-t: probabilistic factors, 2002, p. 8.
- Cryptanalysis of SOBER-t32, 2003, p. 7.
- DA, 2002, pp. 216-222.
- Cryptanalysis of SOBER-t32, 2003, уравнение 11, p. 8.
- Cryptanalysis of SOBER-t32, 2003, p. 8.
- Cryptanalysis of SOBER-t32, 2003, pp. 8—9.
- Cryptanalysis of SOBER-t32, 2003, pp. 9-13.
- Cryptanalysis of SOBER-t32, 2003, pp. 9—10.
- Cryptanalysis of SOBER-t32, 2003, p. 10.
- Cryptanalysis of SOBER-t32, 2003, p. 11.
Литература
- F. Masoodi, S. Alam, M. U. Bokhar. SOBER Family of Stream Ciphers: A Review // International Journal of Computer Applications (0975 – 8887). — 2011. — № 23(1). — P. 1—5.
- M. AlMashrafi, K. Wong, L. Simpson, H. Bartlett, E. Dawson. Algebraic analysis of the SSS stream cipher // Proceeding SIN '11 Proceedings of the 4th international conference on Security of information and networks. — ACM New York, NY, USA, 2011. — P. 199—204.
- P. Hawkes, G. Rose. Primitive Specification and Supporting Documentation for Sober-t32 Submission to NESSIE // Proceedings of the First Open NESSIE Workshop. — 2000.
- S. Babbage, C. De Cannière, J. Lano, B. Preneel, J. Vandewalle. Cryptanalysis of SOBER-t32 // Fast Software Encryption, 10th International Workshop. — 2003.
- P. Ekdahl and T. Johansson. Distinguishing Attacks on Sober-t16 and t32 // Fast Software Encryption 2002. — 2002. — P. 210—224.
- G. Rose. SOBER: A Stream Cipher based on Linear Feedback over GF() // Unpublished report. — QUALCOMM Australia, Suite 410 Birkenhead Point, 1998.
- G. Rose. SOBER II: A Fast Stream Cipher based on Linear Feedback over GF() // Unpublished report. — QUALCOMM Australia, Suite 410 Birkenhead Point, 1998.
- G. Rose. S16 & S32: Fast Stream Cipher based on Linear Feedback over GF() // Unpublished report. — QUALCOMM Australia, Suite 410 Birkenhead Point, 2000.
- G. Rose, P. Hawkes. The t-class of SOBER stream ciphers // Unpublished report. — QUALCOMM Australia, Suite 410 Birkenhead Point, 1998.
- G. Rose, P. Hawkes. Primitive Specifications of SOBER 128. — IACR ePrint Archive, 2003.
- D. Bleichenbacher, S. Patel. SOBER cryptanalysis // Pre-proceedings of Fast Software Encryption ’99. — 1999. — P. 303—314.
- G. Rose. S32: A Fast Stream Cipher based on Linear Feedback over GF() // Unpublished report. — QUALCOMM Australia, Suite 410 Birkenhead Point, 1998.
- S. Babbage, J. Lano. Probabilistic Factors in the Sober-t Stream Ciphers // 3rd open NESSIE Workshop, proceeding. — 2002.
Ссылки
- NESSIE (англ.). — Официальный сайт NESSIE.
- Требования NESSIE (англ.). — Описание основных требований NESSIE.
- Алгоритмы шифрования – участники конкурса NESSIE. Часть 1.
- Алгоритмы шифрования – участники конкурса NESSIE. Часть 2.
- Алгоритмы шифрования – участники конкурса NESSIE. Часть 3.