Шестиугольник Лемуана
Шестиугольник Лемуана[1] представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника.
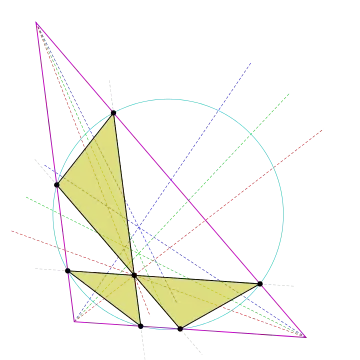
В геометрии (первый) шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника. Есть два определения шестиугольника, которые различаются в зависимости от порядка, в котором соединены вершины.
Площадь и периметр
Шестиугольник Лемуана можно сделать определенные двумя способами, сначала как простой шестиугольник с вершинами в точках пересечения, как определено ранее. Второй способ представляет собой самопересекающийся шестиугольник с линиями, проходящими через точку Лемуана в виде трех ребер, а три других ребра соединяют пары смежных вершин. Для простого самонепересекающегося шестиугольника, построенного внутри треугольника, с длинами сторон и площадью периметр задается в виде:
- ,
а площадь задается в виде:
Для простого самопересекающегося шестиугольника, построенного внутри треугольника, периметр задается в виде:
- ,
а площадь задается в виде:
- .
Описанная окружность шестиугольника Лемуана
В геометрии пять точек определяют коническое сечение, так что произвольные наборы из шести точек, в общем случае вообще не лежат на коническоом сечении, не говоря уже о круге. Тем не менее, шестиугольника Лемуана (либо с порядком подключения) является вписанным в окружность шестиугольником, а это означает, что все его вершины лежат на одной окружности. Окружность шестиугольника Lemoine известна как "первая окружность Лемуана" .
Второй шестиугольник Лемуана
Второй шестиугольник Лемуана[2] представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые антипараллельны сторонам и которые проходят через его точку Лемуана.
Примечания
- Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 109-110, п. 95-96, теоремы, следствие.
- Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 111, п. 98, теорема.
Ссылки
- Casey, John (1888), Lemoine's, Tucker's, and Taylor's Circles, A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples (5th ed.), Dublin: Hodges, Figgis, & Co., с. 179ff, <https://books.google.com/books?id=i87Ikm2u_6sC&pg=PA179>.
- Lemoine, É. (1874), Sur quelques propriétés d’un point remarquable d’un triangle, Association francaise pour l’avancement des sciences, Congrès (002; 1873; Lyon), с. 90–95, <http://gallica.bnf.fr/ark:/12148/bpt6k201149r/f128.image>.
- Mackay, J. S. (1895), Symmedians of a triangle and their concomitant circles, Proceedings of the Edinburgh Mathematical Society Т. 14: 37–103, DOI 10.1017/S0013091500031758.
Внешние ссылки
- Weisstein, Eric W. Lemoine Hexagon (англ.) на сайте Wolfram MathWorld.