Число Ершова

Числа Ершова используются в оптимизации кода для минимизации числа регистров, используемых выражением. Они могут быть использованы в методах оптимального выбора регистров, когда имеется только одно выражение в блоке кода. Если дано выражение E = E₁ операция E₂, то целью является сгенерировать код так, чтобы минимизировать общее число использованных регистров, а в случае недостаточного числа доступных регистров, минимизировать число временных переменных (то есть слов памяти).

Число Ершова n узла заданного дерева выражения определяется следующим образом[1]:

Все листья имеют значение 1.
Число Ершова внутреннего узла с одним дочерним узлом равно числу дочернего узла.
Число Ершова узла с двумя дочерними равно:
а) наибольшему из чисел дочерних узлов, если числа Ершова дочерних узлов различны;

б) числу дочернего узла, увеличенного на 1, если числа Ершова дочерних узлов совпадают.

Число Ершова узла представляет минимальное число регистров, требующихся для выполнения подвыражения, корнем которого является данный узел. Идея заключается в выполнении сначала дочернего выражения с бо́льшим числом Ершова, затем второго дочернего выражения, а после чего операции в корне.

Пример

Дерево выражения

(a-b)+e\times (c+d)

. Справа от узла указаны числа Ершова. Значения a, b, c, d, e — исходные данные, числа tX — промежуточные значения. Пример взят из книги Компиляторы (Ахо, Лам, Сети, Ульман)

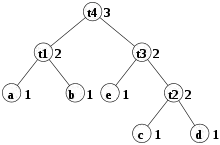
Рассмотрим выражение $(a-b)+e\times (c+d)$ . Пометим узлы дерева (см. рисунок справа) этого выражения метками, равными числам Ершова. Мы имеем операцию '+' в корне, метки левого и правого поддеревьев равные 2, такие, что метка корня равна 3, следовательно, потребуется 3 регистра для реализации выражения.

Каждый из пяти листьев имеет метки "1" (согласно 1-му правилу). Согласно правилу 3, п. "б" узлы t1 и t2 получают метки, равные 2. Теперь узел t3 имеет дочерние узлы с разными метками, так что для него метка будет также 2 (по правилу 3, п. "а"). Узел t4 опять имеет дочерние узлы с равными метками, так что метка для него будет равна 3 (правило 3, п. "б").

Генерация кода

Ниже приведён рекурсивный алгоритм генерации машинного кода[2]. В алгоритме имеется «база» для регистров, то есть для узла с числом Ершова k будут использованы регистры $R_{b},R_{b+1},\dots ,R_{b+k-1}$ :

Для генерации машинного кода внутреннего узла (не листа) с числом Ершова k и двумя дочерними узлами с равными числами (равных k-1) выполняем:
- Создаём код для правого дочернего узла с базой $b+1$ , результат будет помещён в регистр $R_{b+k-1}$ ;
- Создаём код для левого дочернего узла с базой $b$ , результат будет помещён в регистр $R_{b+k-2}$ ;
- Создаём команду «Операция» $R_{b+k-1},R_{b+k-2},R_{b+k-1}$ ;
Пусть рассматривается узел с меткой k и дочерние узлы имеют разные метки. В этом случае один из дочерних узлов имеет метку k, а другой некоторую меньшую метку m. Для такого узла выполняем следующее:
- Создаём код для дочернего узла с бо́льшим числом Ершова, используем базу b, результат будет помещён в регистр $R_{b+k-1}$ ;
- Создаём код для другого дочернего узла, используем базу b, результат будет помещён в регистр $R_{b+m-1}$ ;
- Создаём команду «Операция» $R_{b+k-1},R_{b+m-2},R_{b+k-1}$ или «Операция» $R_{b+k-1},R_{b+k-1},R_{b+m-1}$ (зависит от того, где находится узел с бо́льшим числом Ершова);
Для листового узла с операндом x создаём команду «Загрузить» $R_{b},x$ .

Вычисление выражений при недостаточном числе регистров

Если число Ершова корневого узла выражения больше доступного числа регистров, то число Ершова может быть использовано для генерации кода с минимальным числом операций загрузки и сохранения следующим образом[3]

Для корня выполняем

Создаём код для дочернего узла с бо́льшим числом Ершова;
Создаём команду сохранения результата в памяти;
Создаём код для дочернего узла меньшим числом Ершова;
Создаём инструкцию загрузки запомненного значения в регистр;
Создаём команду, выполняющую операцию в корне.

См. также

Число Стралера — Философова, минимальное число регистров, необходимых для выполнения выражения без внешней памяти
Алгоритм Сети — Ульмана, по существу, та же концепция

Примечания

Ахо, Лам, Сети, Ульман, 2008, с. 689-692.
Ахо, Лам, Сети, Ульман, 2008, с. 690.
Ахо, Лам, Сети, Ульман, 2008, с. 692-693.

Литература

Альфред В. Ахо, Моника С. Лам, Рави Сети, Джеффри Д. Ульман. 8.10.1 Числа Ершова // Компиляторы (принципы, технологии и инструментарий). — Москва, Санкт-Петербург, Киев: «Вильямс», 2008. — ISBN 978-5-8459-1349-4.

Ссылки

Carleton University page on Optimal Code Generation and using Ershov numbers.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_23b38e38d5ebefba-1] Ахо, Лам, Сети, Ульман, 2008, с. 689-692.

[_646e84564dc3c1bc-2] Ахо, Лам, Сети, Ульман, 2008, с. 690.

[_9424f28b4c35cbd3-3] Ахо, Лам, Сети, Ульман, 2008, с. 692-693.