Тропическая геометрия

Тропические кривые второй степени (в разных масштабах). Показаны соответствующие многочлены. Числа у рёбер показывают их кратность, если она не соответствует их наклону.

Тропические кривые третьей степени.

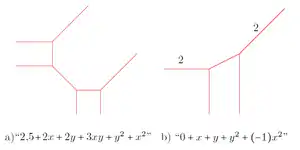
• Тропическое полукольцо (или тропическое полуполе) — множество вещественных чисел ${\displaystyle \mathbb {R} }$, снабжённое операциями тропического сложения ${\displaystyle \oplus }$ и тропического умножения ${\displaystyle \odot }$

${\displaystyle x\oplus y=\max(x,y),\quad x\odot y=x+y.}$

• Тропический многочлен степени ${\displaystyle d}$ на плоскости — кусочно-аффинная функция вида

${\displaystyle f(x,y)=\bigoplus _{i+j\leq d}\,a_{i,j}\odot x^{\odot i}\odot y^{\odot j}=\max _{i+j\leq d}(ix+jy+a_{i,j}).}$

Аналогично, тропический многочлен в общем случае — кусочно-аффинная функция вида

${\displaystyle f(x_{1},\dots ,x_{n})=\bigoplus _{|J|\leq d}\,a_{J}\odot x^{\odot J}=\max _{|J|\leq d}\,(a_{J}+\sum _{i}J_{i}x_{i}).}$

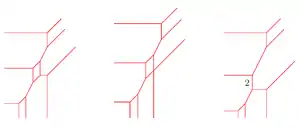
• Тропическая кривая на плоскости, соответствующая данному тропическому многочлену ${\displaystyle f}$ степени ${\displaystyle d}$ — граф на плоскости, вершины и рёбра (конечные и бесконечные) которого образуют множество точек негладкости функции ${\displaystyle f}$. Рёбра этого графа считаются снабжёнными кратностями: ребро, разделяющее области линейности, отвечающие набору степеней ${\displaystyle (i,j)}$ и ${\displaystyle (i',j')}$, снабжается кратностью, равной наибольшему общему делителю разностей ${\displaystyle i-i'}$ и ${\displaystyle j-j'}$.
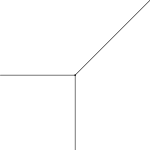
• В частности, тропическая прямая есть объединение трёх лучей, исходящих из некоторой точки ${\displaystyle (x_{0},y_{0})}$ и направленных вниз, влево и вправо-вверх под 45°. Тропические прямые обладают свойствами, аналогичными свойствам обычных прямых: через любые две точки общего положения проходит ровно одна тропическая прямая, и две тропические прямые общего положения пересекаются в единственной точке.

• Itenberg I., Mikhalkin G., Shustin E. Tropical algebraic geometry. — Basel: Springer, 2009. — viii+104 с. — (Oberwolfach Seminars).

• М. Э. Казарян. Тропическая геометрия. — М.: МЦНМО, 2012. — 43 с. — (Летняя школа «Современная математика»). — 1000 экз. — ISBN 978-5-94057-966-3.