Теорема Гарнака о кривых

Теорема Гарнака о кривых, названная именем Акселя Гарнака, даёт возможное число связных компонент, которое может иметь алгебраическая кривая в терминах степени кривой. Для любой алгебраической кривой степени m на вещественной проективной плоскости число компонент c ограничено выражением

${\displaystyle {\frac {1-(-1)^{m}}{2}}\leqslant c\leqslant {\frac {(m-1)(m-2)}{2}}+1.\ }$

Эллиптическая кривая (степени 3) слева является M-кривой, поскольку имеет максимум (2) компонент, в то время как кривая справа имеет только одну компоненту.

Максимальное число компонент на единицу больше максимального рода кривой порядка m, достигаемого в случае несингулярности кривой. Более того, любое число компонент в этом диапазоне возможных значений может быть достигнуто.

Кривая Тротта с показанными здесь 7 касательными является квартикой (степени 4), M-кривой, достигающей максимального числа (4) компонент для кривых такой степени.

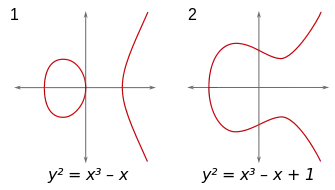
Кривая, достигающая максимального числа вещественных компонент, называется M-кривой (от «maximum») . Например, эллиптическая кривая с двумя компонентами, такая как ${\displaystyle y^{2}=x^{3}-x,}$ или кривая Тротта, квартика с четырьмя компонентами, являются примерами M-кривых.

Эта теорема образует предпосылки для шестнадцатой проблемы Гильберта.

В современных исследованиях показано, что кривые Гарнака — это кривые, амёба которых имеет площадь, равную многоугольнику ньютона многочлена P, который называется характеристической кривой димерных моделей, и любая кривая Гарнака является спектральной кривой некоторой модели димеров[1][2].