Спектральная плотность излучения

Спектра́льная пло́тность излуче́ния — термин в фотометрии и теории электромагнитных волн, под которым, в зависимости от контекста, может пониматься одна из следующих физических величин:

• спектральная объёмная плотность энергии излучения, то есть характеристика области пространства, в которой наличествует электромагнитное излучение. Такая величина рассчитывается как

${\displaystyle u_{\nu }=<{\frac {dW}{dVd\nu }}>\quad }$ (вариант: ${\displaystyle u_{\lambda }=<{\frac {dW}{dVd\lambda }}>}$),

где ${\displaystyle W}$ — энергия, ${\displaystyle V}$ — объём, ${\displaystyle \nu =\omega /2\pi }$ — частота (Гц) и ${\displaystyle \lambda }$ — длина волны излучения;

• спектральная поверхностная плотность мощности излучения (также: спектральная излучательная или испускательная способность), то есть характеристика излучающей поверхности рассматриваемого тела. Эта величина определяется как

${\displaystyle I_{\nu }=<{\frac {dP}{dSd\nu }}>\quad }$ (вариант: ${\displaystyle I_{\lambda }=<{\frac {dP}{dSd\lambda }}>}$),

где ${\displaystyle P}$ — мощность, а ${\displaystyle S}$ — площадь излучателя. Фактически это средняя плотность потока энергии в узком интервале частот (или длин волн), отнесённая к величине интервала.

Усреднение производится по большому промежутку времени. Упомянутые величины ${\displaystyle u}$ и ${\displaystyle I}$ связаны соотношением ${\displaystyle u=4/c\cdot I}$, где ${\displaystyle c}$ — скорость света. Ниже для определённости рассматривается ${\displaystyle I}$. Общепринятых буквенных обозначений для обсуждаемых величин нет, однако принято вводить дополнительный значок, указывающий на аргумент, по которому берётся интервал и от которого зависит спектральная плотность: ${\displaystyle I_{\nu }(\nu )}$ или ${\displaystyle I_{\lambda }(\lambda )}$.

Спектрограммы двух источников света: слева — лампа накаливания, справа — флюоресцентная лампа. По горизонтали отложена длина волны ${\displaystyle \lambda }$ в нм (видимый диапазон; соответствующие цвета показаны). Чёрный график — спектральная плотность излучения ${\displaystyle I_{\lambda }(\lambda )}$.

Смотря по тому, частота или же длина волны выбрана в качестве аргумента, спектральная плотность излучения ${\displaystyle I}$ в СИ будет измеряться в (Вт/м²)/Гц или в (Вт/м²)/м. Аналогично для ${\displaystyle u}$: в (Дж/м³)/Гц или в (Дж/м³)/м.

Поскольку частота и длина волны связаны как ${\displaystyle \lambda \nu =c}$, переход от ${\displaystyle I_{\nu }(\nu )}$ к ${\displaystyle I_{\lambda }(\lambda )}$ осуществляется через

${\displaystyle I_{\lambda }(\lambda )=I_{\nu }(c/\lambda )\cdot c/\lambda ^{2}}$.

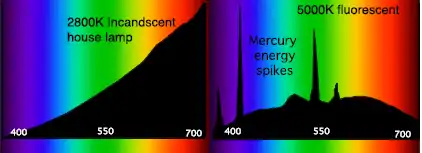
Обычно (см. примеры на рисунке) энергия излучения неравномерно распределена по волнам различных длин. Поэтому спектральная плотность излучения сложным образом зависит от выбранного аргумента (в данном примере — длины волны).

Для некоторых типов источников излучения их спектральная плотность известна из фундаментальных принципов. Так, для абсолютно чёрного тела

${\displaystyle I_{\nu }={\frac {2\pi h\nu ^{3}}{c^{2}}}{\frac {1}{e^{h\nu /kT}-1}},\qquad I_{\lambda }={2\pi h{c^{2}} \over \lambda ^{5}}{1 \over e^{hc/\lambda kT}-1}}$,

где ${\displaystyle T}$ — температура, а ${\displaystyle h}$ — постоянная Планка. Спектр лампы накаливания (левая часть рисунка) в видимой области достаточно хорошо описывается этими формулами.

Полная интенсивность излучения (без слова «спектральная») получается путём интегрирования ${\displaystyle I}$ по выбранному аргументу.