Слабая раскраска

Слабая раскраска — это специальный вид разметки графа. Слабая k-раскраска графа G = (V, E) назначает цвета c(v) ∈ {1, 2, ..., k} всем вершинам v ∈ V, так что каждая неизолированная вершина смежна по меньшей мере одной вершине другого цвета. В формальных обозначениях, для любой неизолированной вершины v ∈ V существует вершина u ∈ U с {u, v} ∈ E и c(u) ≠ c(v).

Слабая 2-раскраска.

Рисунок справа показывает слабую 2-цветную раскраску графа. Каждая тёмная вершина (цвет 1) смежна по меньшей мере с одной светлой вершиной (цвет 2) и наоборот.

Построение слабой 2-раскраски.

Свойства

Раскраска вершин графа является слабой раскраской, но обратное не обязательно верно.

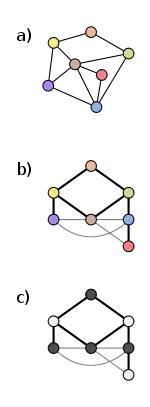
Любой граф имеет слабую 2-раскраску. Рисунок справа показывает простой алгоритм построения слабой 2-раскраски произвольного графа. Фрагмент (a) показывает исходный граф. Фрагмент (b) показывает дерево поиска в ширину того же графа. Фрагмент (c) показывает, как раскрасить дерево — начиная с корня, уровни дерева раскрашиваются попеременно цветом 1 (тёмный) и 2 (светлый).

Если нет изолированных вершин в графе G, то слабая 2-раскраска определяет доматическое разбиение — множество вершин с c(v) = 1 является доминирующим множеством, а множество вершин с c(v) = 2 является другим доминирующим множеством.

Приложения

Исторически, слабая раскраска выступила в качестве первого нетривиального примера задачи на графе, которая может быть решена локальным алгоритмом (распределённым алгоритмом, работающим за постоянное число раундов синхронной передачи). Точнее, если степень каждой вершины нечётна и ограничена константой, то существует распределённый алгоритм слабой 2-раскраски с постоянным временем работы [1].

Данный случай отличается от (не слабой) раскраски вершин — не существует распределённого алгоритма раскраски вершин с постоянным временем работы. Лучшие возможные алгоритмы (для поиска минимальной, но не обязательно наименьшей по количеству цветов раскраски) требуют O(log* |V|) раундов передачи [1][2][3]. Здесь log* x — итерированный логарифм от x.

Примечания
  1. Naor, Stockmeyer, 1995, с. 1259–1277.
  2. Linial, 1992, с. 193–201.
  3. Cole, Vishkin, 1986, с. 32–53.

Литература
  • Moni Naor, Larry Stockmeyer. What can be computed locally? // SIAM Journal on Computing. — 1995. — Т. 24, вып. 6. — С. 1259–1277. — doi:10.1137/S0097539793254571.
  • Nati Linial. Locality in distributed graph algorithms // SIAM Journal on Computing. — 1992. — Т. 21, вып. 1. — С. 193–201. — doi:10.1137/0221015.
  • Richard Cole, Uzi Vishkin. Deterministic coin tossing with applications to optimal parallel list ranking // Information and Control. — 1986. — Т. 70, вып. 1. — С. 32–53. — doi:10.1016/S0019-9958(86)80023-7.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.